тогда, когда положительно скалярное произведение ys, а оно по построению равно 1/5. Значит, для того чтобы BFGS-фор-мула сохраняла положительную определенность, необходимо и достаточно выполнения неравенства

yls,>0. (4.41)

Неравенство (4.41) будет выполнено, если выбирать шаги «д па основе «достаточно аккуратного» одно.мерного поиска. В самом деле, по определению имеем

Поскольку (прн положительно определенной Вд) является направлением спуска, величина ~в1рк и шаг в правой части равенства положительны. Отрицательным может быть только скалярное произведение gl+p„, но, повышая точность одномерной минимизации, его всегда можно сделать сколь угодно близким к нулю (так как gluPi, обращается в нуль, если -точное решение задачи м)тни.мизации F вдоль р;.). Тогда сумма в скобках и величина j/Js станут положительными, что и требовалось установить.

Конечная сходимость для квадратичных функций. Подчиняя очередное приближение В+, матрицы Гессе квазиньютоновскому условию Bft4,Se = i/ft, "Ь! добиваемся, чтобы это приближение правильно отражало кривизну F вдоль определеннто направления. Однако последующие модификации B+t Могут приводить к утрате данного свойства. Для того чтобы приобретаемая информация о кривизне сохранялась в течение нескольких итераций, т. е. для некоторых / (/ А) было обеспечено равенство

надо принимать специальные меры. Когда квазиньютоновский поиск используется для минимизации квадратичной формы, соблюдение равенства (4.42) для п линейно независимых векторов {s,} гарантирует, что на (n-l-I)-M шаге будет найдено точное решение. Действительно, пусть G - матрица Гессе минимизируемой формы, а S - патрица, 1-й столбец которой равен s,. Тогда (4,42) преобразуется к виду

S„.sS = GS,

где учтено, что j, = GSi, Поскольку S по предположению невырождена, отсюда следует, что В„., = С, а это значит, что (пЧ- 1)-й шаг будет ньютоновским, т, е. приведет в точку минимума.

Если применить для минимизации квадратичной функции какую-нибудь формулу из однопараметрического семейства (4,35) и иа каждой итерации точно решать задачу одномерного поиска, то

ДЛЯ ys=0.....п-1 гарантированы соотношения

B„sj=yj, j<k: sfGsjO, ij.

Второе из них обеспечивает линейную независимость векторов {Sj} и тем самым конечную сходимость мегода. Таким образом, все квазиньютоновские формулы из (4,35) дают минимум квадратичной функции за конечное число шагов, и для всех последнее приближение матрицы С (есаи она невырождена) совпадает с ней, хотя промежуточные приближения Bft для разных формул из (4,35) будут разными.

4.5.2.2. Реализация. Направления поиска Рл и в ньютоновских, и в квазиньютоновских методах определяются в результате решения некоторых систем линейных уравнений. В ньютоновских методах это - системы с матрицами Гессе G. Последние вычисляются на разных итерациях совершенно независимо друг от друга, и поэтому расчет рд всякий раз приходится начинать «с нуля». Точнее говоря, чтобы найти pft, на каждой итерации приходится заново строить какое-то матричное разложение. Иначе дело обстоит с квазиньюто-новскшчи методами. В них матрица очередной системы для построения рд отличается от предыдущей лишь поправкой малого ранга. В данном случае каждый раз заново строить ее разложение неэкономно (см, разд, 2,2.5,7),

Проблему эффективной организации расчета направлений квазиньютоновского поиска можно решать по-разному. Авторы первых квазиньютоновских алгоритмов делали это просто: они отказывались от системы (4,28), конструируя такие процедуры, которые оперируют приблшкеииями не самой матрицы Гессе, а обратной к ней матрицы. Соответствующие формулы пересчета выводились независимо от рассмотренных в предыдуи;эм разделе, но могут быть получены и из них как формулы пересчета матриц В, Когда метод минимизации строится на квазиньютоновских приближениях Яд обращенной матрицы Гессе, направления поиска рд вычислягсггся по формуле

Pn=-HbgH, (4.43)

а квазиньютоиовское условие принимает вид равенства

«.+1г/* = 8.- (4,44)

На первый взгляд может показаться, что переход к аппроксимации обращенной матрицы Гессе сулит значительное упрощение расчета направления поиска, поскольку решение системы (4,28) «с нуля» требует порядка п? операций, в то время как число операций, необходимых для вычисления матрично-вектор-ного произведеиия в (4,43), пропорционально Tf-. Однако приведенная оценка трудоемкости построения p, в методе с аппроксимацией прямой матрицы Гессе относится только к самому примитивному способу организации вычислений. Эта оценка

будет совсем иной, если вместо явной формы задания квази-ньютоновских матриц использовать их разложения Холесского. Коль скоро LDi.-разложение матрицы Вц известно, число операций, необходимых для решения системы (4.28), будет кратно п*, причем трудоемкость расчета факторов Lj+i и D+i матрицы получающейся из Вд квазиньютоновской модификацией малого ранга, оказывается примерно такой же, как и трудоемкость расчета очередной матрицы (см. разд. 2.2.5.7).

Имея разложения Холесского матриц В,,, можно получать полезные оценки их чисел обусловленности. Например, нетрудно показать, что если максимальный и минимальный диагональные элементы фактора Сд равны d„„ и d„i„, то справедливо неравенство cond(Bt)>d„„/dmin- В момент завершения процесса минимизации оценка числа обусловленности позволит дать заключение о пригодности полученного приближенного решения (см. разд. 8.3 3). На промежуточных итерациях такие оценки нужны для выявления ситуаций, когда матрица Вд обусловлена столь плохо, что в численном решении рд системы (4.28) скорее всего не окажется ни одной правильной цифры. При этом факторы разложения легко подправить так, что обусловленность результирующей матрицы станет приемлемой. Подобные корректировки являются одновременно и средством достижения глоба.дьной сходимости (см. разд. 4.5.2.3).

Подключение факторизации Холесского позволяет избежать еще одной неприятной проблемы, которая часто оказывается камнем преткновения для обычных квазииьютоновских методов. Имеется в виду проблема потери (из-за ошибок округления) положительной определенности квазиньюпюновских матриц. В теоретических дискуссиях она часто замалчивается, но для практиков очень важна, и в особенности, если говорить о задачах минимизации функций сложной структуры. С точки зрения теории гарантировать положительную определенность нетрудно. Например, для BFGS-формулы (4.37) достаточно соблюдать неравенство (4.41). Однако на самом деле нередко случается, что это неравенство выполнено, а вычисленная квазиньютоновская матрица из-за погрешностей машинной арифметики оказывается знаконеопределенной.

Пример 4.8. Рассмотрим двумерный случай с матрицей

В. =

и пусть 5д = (1, 10-)г, й = (0. 1)- Неравенство tlSk>0 соблюдено, т. е. пересчет Вд по BFGS-формуле должен дать положительно определенную матрицу. Тем не менее, если вычисления провести на машине с пятиразрядной десятичной точностью, результатом этого пересчета будет матрица с нулем в (1,1)-й позиции, а это исключает положительную определенность. При

абсолютно точных вычислениях в данной позиции стояло бы малое положительное число, но при расчетах с ошибками округления оно теряется.

Утрата положительной определенности нежелательна не только из-за того, что вектор рд в этом случае может указывать в сторону возрастания минимизируемой функции, но и потому, что она чревата внесением в квазиньютоновскую аппроксимацию бессмысленных поправок, уничтожающих накопленную информацию о кривизне F. При этом по даиньш функционирования обычного (без факторизации) квазиньютоновского алгоритма уловить момент, когда матрица Ви перестала быть положительно определенной, иногда просто невозможно: индикаторами здесь служат векторы рд, а они могут оставаться направлениями спуска и в отсутствие положительной определенности Вд. Если же в таком алгоритме потеря положительной определенности выявлена, то, как правило, приходится возвращаться к единичной матрице, стирая тем самым полезную информацию о кривизне F. Короче говоря, при реализации квазиньютоновского подхода очень важно позаботиться о численной положительной определенности приближений матрицы Гессе (или обратной к ней матрицы).

Коль скоро квазиньютоновский поиск организуется с привлечением факторизации Холесского, избежать потери положительной определенности нетрудно. Здесь все зависит от значений диагональных элементов фактора Dj,: пока они больше нуля, положительная определенность соответствующей квазиньютоновской матрицы гарантирована. Контролируя эти значения при пересчете диагонального фактора, мы всегда выявим опасность потери положительной определенности в тот самый момент, когда она возникнет, и сможем принять своевременные меры.

На рис. 4т изображена траектория квазиныотоновского поиска при минимизации функции Розенброка (пример 4.2). Для аппроксимации матрицы Гессе использовалась BFGS-формула, а шаги пд определялись как аккуратные приближения точек минимумов по направлениям спуска. Отметим, что, как и ньютоновский метод, алгоритм обеспечивает быстрый прогресс вдали от решения. Затруднения возникают только в окрестности начала координат, где кривизна минимизируемой функции меняется наиболее быстро.

*4.5.2.3. Сходимость; экстремальность квазиньютоновских поправок. В данном разделе приводится перечень некоторых интересных свойств квазиньютоновских методов. Более полные сведения читатель найдет по ссылкам, данным в замечаниях.

Глобальная сходимость квазиньютоновского поиска к стационарной точке может быть доказана для дважды непрерывно дифференцируемой функции F в следующих предположениях: (i) множество HF(x) ограничено; (ii) матрицы положительно определены и нх числа обусловленности равномерно ограничены; (iii) выбор шагов

ад осуществляется на основе какого-нибудь из критериев разд. 4.3.2.1. Требование к матрицам Вд гарантирует, что угол между направлением поиска и антиградиентом всегда будет отличаться от прямого не менее чем на некоторую ненулевую константу. Если {Вд} генерируются процедурой с использованием разложений Колесского (см. разд. 4.5.2.2), удовлетворить этому требованию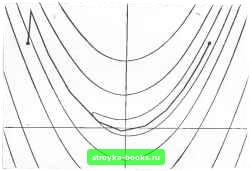

Рис. 4т. Траектория поиска минимума функции Розенброка квазиньютоиовским методом с BFGS-формулой.

нетрудно, так как в правилах пересчета факторов можно предусмотреть контроль числа обусловленности и (выполняемые по мере необходимости) корректировки, непосредственно ограничивающие его значение.

Если же матрицы Вд всегда вычисляются по какой-то обычной квазнньютоновской формуле и никакого явного средства ограничения их чисел обусловленности не используется, то для доказательства сходимости придется усилить предположения о способе выбора шагов ад и о свойствах минимизируемой функции. Так, например, сходимость квазиньютоновского процесса с применением какой-нибудь из формул однопараметрического семейства (4.35) может быть доказана в предположении, что одномерный поиск осуществляется точно и собственные значения матрицы Гессе минимизируемой функции равномерно по х ограничены сверху и снизу положительньшн константами. Сходимость при выборе ад на основе приближенной одномерной минимизации пока удалось доказать только для BFGS-формулы. Точнее говоря, установлено, что соответствующий метод сойдется, если вычислять a, согласно критериям (4.7) н (4.8), причем довольно неестественное предположение относительно соб-

ственных чисел матрицы Гессе пришлось сохранить. (Читатель, наверное, догадывается о том, что требования, предъявляемые к минимизируемой функции, обусловлены в основном сложностью доказательств и не отражают реальных возможностей квазиньютоновских методов. На самом деле класс функций, для которых они сходятся, значительно шире оговариваемого в формулировках теорем сходимости.)

Наряду с работами, посвященными вопросам существования сходимости квазиньютоновских методов, немало усилий было затрачено и на исследование скоростей их сходитюсти. Мы снова ограничимся краткой сводкой результатов, а более полные сведения можно найтн в рекомендуемой ниже литературе.

Некоторые свойства сходимости квазиньютоновских методов удается получить анализом общей итерационной схемы, в которой

Xkii = Xk + PH. (4.45)

где Pk удовлетворяет равенству BkPh~-gh Заметьте, что в этой схеме длина шага вдоль равна единице. При необременительных предположениях относительно матриц Sj, (выполненных, в частности, для BFGS-, PSB- и DFP-формул) и минимизируемой функции F можно доказать следующее: если в стационарной точке х* матрица G(x*) положительно определена и Хц, Во «достаточно близки» к д:*, G(x*) соответственно, то последовательность (4.45) линейно сойдется к X*. Свойство, которое требуется от матриц 6д при доказательстве этой локальной сходимости, называют ограниченной изнашиваемостью, применительно к перечисленным выше формулам оно проявляется в виде неравенств

(x«)KvJiB,-G (x«)+(l+Y,)птах {х.-х«, х,.~х«}.

Здесь Yi и уя- некоторые неотрицательные константы, а выбор норм не конкретизирован, поскольку разным формулам пересчета отвечают разные нормы.

В определенных условиях квазиньютоновские методы сходятся сверхлинейно. При выводе таких условий обычно учитывают, что для сходящейся сверхлинейно последовательности {хд} должно выполняться соотношение

(4.46)

В этом можно убедиться на примере с квадратично сходящейся к нулю последовательности чисел 10"*, 10", 10"" и т. д.

Если известно, что последовательность точек, генерируемая по схеме (4.45), сходится с линейной скоростью, то для того, чтобы сходимость на самом деле была сверхлинейной, необходимо и достаточно, чтобы матрицы Bj удовлетворяли условию

(4.47)