По определению Ф для любых точек x,-+i и х, связанных равенством

Х1+1 = Х1 + а.ф1,

&•+, -= С (х,+, -х,) = а, Ср,.

(4.84)

(4.85)

Из этой формулы следует, что g,, есть линейная комбинация направлений рл, pi, . ... рк. Аналогично и gj для i<h будет линейной

комбинацией от ро, р,.....р;. Поэтому, учитывая (4,80), можно

утверждать, что

gfe = 0, i<k. (4.86)

Чтобы выяснить, какие коэффициенты (3, обеспечивают сопряженность рд всем предыдущим направлениям р,., умножим (4.85) на р]С:

Pi GPk = -pJ Ggk + Д Р»Х Ср,. =

(4.87)

Обозначив разность g,-+i-g, через у,., получим, что условие сопряженности pTGpj = 0 эквивалентно условию ортогональности yjpj = 0. Это понадобится нам в дальнейшем.

Мы установили, что среди методов минимизации квадратичных функций (4.77), ук-ладывающихся в общую схему спуска из разд. 4.3.1, есть метод, k-я итерация которого приводит в точку минимума Ф на многообразии Xk i+Sk-t- Теоретически этот метод конечен: при точных вычислениях он должен найти решение не более чем за п шагов, поскольку многообразие x„ i+5„ , совпадает со всем пространством значений аргумента х, и, следовательно, если оптимальная точка не была найдена ранее, то она во всяком случае будет найдена на п-м шаге. Чтобы окончательно определить метод, надо задать правило построения взаимно сопряженных направлений {pj\. Мы покажем сейчас, что направление рд для очередной итерации можно вычислять как линейную комбинацию градиента в текущей точке Хк и предьщущего направления p,, i. Доказательство проведем по индукции.

Пусть ро совпадает с антиградиентом -go в начальной точке Хо и k шагов метода (4.83) спуска по взаимно сопряженным направлениям Ро, р,.....pft , уже выполнены, причем каждый из векторов pi был суммой антиградиента -g,. и линейной ко.мбипацни от ро. Pi, . . ., Pi-i. Направление рд для очередного шага тоже будем искать в виде

Здесь использованы равенство (4.84) и предположение о взаимной сопряженности направлений Ро, .,., p.j. В силу (4.86) при i < k- 1 первое слагаемое правой части (4.87) обращается в нуль, и поэтому, чтобы обеспечить взаимную сопряженность и р; при i < к- 1, надо взять соответствующие Pj, нулевыми. Таким образом, ненулевым среди множителей в (4.85) может быть только Рк.к-1- Впредь будем обозначать его через Рд ,-. Л\ножитель Pj j надо подобрать так, чтобы вектор рд был сопряжен к pj j. Для этого достаточно удовлетворить условию ортогональности J/Lipb = 0. Соответственно, умножив (4.85) на Ук1 и приравняв левую часть полученного равенства нулю, находим, что искомый множитель должен быть решением уравнения

О = - Ук-iSk + Pt-iyLiPt-i,

(4.88)

Итак, в качестве векторов р,, для (4.83) следует брать

Р* = -gft + Pb-iPt-i. (4-89)

где Рд 1 вычислягсгтся по формуле (4.88). Взаимная ортогональность градиентов и определение p i позволяют предложить еще две внешне отличные от (4.88), но теоретически эквивалентные ей формулы расчета Pt i:

4.8.3.2. Линейный метод сопряженных градиентов. На описанный в предыдущем разделе метод минимизации квадратичных функций можно смотреть и как на метод решения систем линейных уравнений с положительно определенными матрицами-ведь, отыскав минимум для Л-Ь VsxGx, мы тем самым найдем решение системы

Gx=-с. (4.90)

Именно в таком качестве он был опубликован впервые. Когда о методе сопряженных градиентов говорят как о процедуре решения линейных систем, к его названию добавляют эпитет «линейный». Замечательная особенность данного метода состоит в том, что для поиска решения системы ему требуются только произведения ее матрицы на некоторые векторы и не нужна сама матрица. Это означает, например, что если G представлена произведением то при обращении к методу сопряженных градиентов явно формировать элементы этого произведения ие понадобится.

В описаниях линейного метода сопряженных градиентов суммы c-hCXj (градиенты функции (4,77)) принято обозначать через г.

и называть невязками. На k-li итерации последовательно вычисляются

Pfi = - (i + Pt+iPs-i;

»+1 = -ь + «*<Зрд;

(4.91)

Чтобы запустить метод, надо задать начальное приближение Хс и отвечающую ему невязку Га=с+Сх„. Величины p i и p i, фигурирующие в (4.91) при /г=0, полагаются нулевыми.

Теоретически линейный метод сопряженных градиентов должен найти точное решение системы (4.90) за число итераций, не превышающее размерности вектора неизвестных. Точнее говоря, при вычислениях без погрешностей решение будет получено за т<п шагов, где m - число различных собственных значений матрицы G. Таким образом, метод можно считать конечным. Однако если исходить из практических соображений, то его скорее следует отнести к классу итерационных методов, поскольку при реализации на машине он редко дает удовлетворительное решение за п шагов. Это связано с тем, что из-за неточностей машинной арифметики сопряженность вычисляемых направлений рд быстро теряется. Когда собственные значения матрицы О/, распадаются на группы почти одинаковых чисел, линейный метод сопряженных градиентов может сойтись очень быстро; если же подобной структуры собственных значений нет, для определения хорошего численного приближения ему может потребоваться значительно больше, чем п итераций.

4.8.3.3. Нелинейные функции общего вида. Метод сопряженнь1х градиентов из разд. 4.8.3.1 легко обобщается на задачи минимизации нелинейных функций общего вида. Для этого надо заменить используемую в нем формулу расчета какой-нибудь процедурой одномерного поиска и уточнить, будет ли направление рд всегда вычисляться по формуле (4.89) или допускаются периодические отступления. Последние принято называть рестартами или восстановлениями. Можно, например, принимая во внимание п-шаго-вую теоретическую сходимость в квадратичном случае, через каждые п шагов отказываться от направления (4.89) и брать в качестве очередного Рд антиградиент -gh. Соответствующий метод называют традиционным.

Траектория традиционного метода сопряженных градиентов в задаче минимизации функции Розенброка (пример 4.2) изображена на рис. 4о. Хотя этот метод не предназначен для решения задач столь малой размерности, приведенная иллюстрация все же полезна.

поскольку показывает его циклический характер. Отметим, что он работает значительно лучше, чем наискорейший спуск, и хуже, чем квазиньютоновскнй метод с BFGS-формулой (см. рис. 4j и 4гп).

Определение точного (в машинном смысле) минитмума F{x) вдоль Рд в общем случае требует больших усилий. Поэтому многие реализации традиционного метода сопряженных градиентов допускают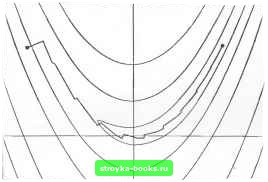

1 НС. 40. "1 раекторин поиска минимума функции Розенброка методом сопряженных градиентов.

приближенный одномерный поиск. Здесь, однако, приходится специально позаботиться о том, чтобы вектор рд всегда был направлением спуска. При точном одномерном поиске это условие соблюдается автоматически - оно оказывается следствием вытекающего из (4.89) равенства

glpt = - glgk + [\-,gIPk-i Если минимум вдоль рд 1 найден точно, скалярное произведение gkPk-i равно нулю, и поэтому величина §дРд, совпадающая < -glgk, будет отрицательной. Если же одномерный поиск ведется приближенно, то произведение Pk-ygkPk-i может оказаться положительными превосходящимд. Тогда рд будет указывать в сторону возрастания F (х). Чаще всего на этот случай предусматривают возможность внеочередного рестарта, заменяя неудачное направление антиградиентом. Надо только иметь в виду, что, если такие замены из-за слишком примитивной организации одномерного поиска станут очень частыми, метод практически превратится в алгоритм наискорейшего спуска, т. е. станет совершенно неэффективным.

Проблему обеспечения правильной ориентации векторов рд при неточном одномерном поиске можно решать и по-другому, вводя в алгоритм выбора шага дополнительное условие. Формулируется оно следующим образом. Обозначив через gs+„ р., и Рд значения величин gj+„ Ps+, н Рд в точке х„-\-ар, где а -пробный шаг одномерного попска, будем считать, что а/ может претендовать на роль а,, только в том случае, если при некотором малом положительном о выполнено неравенство

-gLlPнг>o(gk.l ILIP*+jL (4.92)

Если же оно не выполняется нн прн одном пробном а, то одномерный поиск будем вести до тех пор, пока не будет найдец точный минимум F {X) вдоль рд. При таком ограничении на выбор Пд правильная ориентация р+д гарантирована.

Поскольку направ.тенне рд ц в методе сопряженных градиентов определяется просто, проверка неравенства (4.92) лишь незначительно усложнит процедуру одномерного поиска. Заметим, кстати, что формировать р., явным образом не обязательно, так как величины gJ-fiPj+i н рд ц легко вычисляются noghigk+i, Pft и St+iPk- Ну а еслн критерию приемлемости шага удастся удовлетворить с первой попытки, то о дополнительных затратах иа проверку (4.92) вообще говорить не приходится: в данном случае все связанные с ней величины все равно пришлось бы вычислить для других це.11ей.

4.8.3.4. Методы сопряженных градиентов с рестартами. Когда реализация схемы сопряженных градиентов предполагает периодические возвраты (рестарты) к направлениям наискорейшего спуска, то выигрыш на итерации рестарта почти всякий раз оказывается меньше того, который был бы получен, еслн бы рестарта не было. Это связано с тем, что антиградиент, как правило, яапя-ется неудачным направлением спуска. Соответственно возникает желание переключаться не на него, а на какое-то другое направление, например начинать очередной цикл из п итераций с последнего направления предыдущего цикла. Однако здесь нужна некоторая осторожность.

Если в нелинейном методе сопряженных градиентов взять в качестве начального направления р„ произвольный вектор, то взаимной сопряженности между генерируемыми им направ.теннями, вообще говоря, не будет, так как g„ не будет нх линейной комбинацией. Чтобы сохранить сопряженность, вместо (4.89) надо использовать формулу вида

Pi, = - gk +k-iPb-i +YftP«.

(4.93)

г№. yk=yIgklyiPb< а Pj i по-прежнему вычисляется по формуле (4.68). Обобщение данного подхода для задач с неквэдратичнымн

функциями состоит в том, чтобы на очередном цикле из п итераций строить направления рц, А = 0, п-1, по правилу

Р» = -et+Pt-iPt-i+VoPc

(4.94)

где Ук ylgklyTPf а Pt-последнее направление предшествующего цикла. Вектор р, принято называть направлением рестарта.

Счедует отметить, что рд из (4.94) может указывать в сторону возрастания F(x) даже в том случае, еслн подзадача одномерной М1ши-мизации вдоль Рй 1 решена точно. Значит, обращаясь к (4.94), надо предусмотреть возможность аварийных рестартов - замены неприемлемого Рь нз (4.94) вектором, вычисленным по обычной формуле. При этом «хорошим» направлением Рк естественно считать такое, вдоль которого минимизируемая функция убывает «достаточно быстро». Например, можно ввести аналогичное (4.92) условие вида

-elPk>eW.\\gkK. тле р-некоторое положительное число, н каждый раз, когда для рд из (4.94) оно нарушится, начинать новый цикл итераций с рд , в качестве направления рестарта и с рд, пересчитанным в соответствии с формулой (4.89).

Когда одномерный поиск осуществляется точно, правильная ориентация рд при описанном способе аварийного рестарта гарантирована. Если же используется приближенный поиск, то на итерациях рестарта (как аварийного, так и обычного) точка минимума вдоль Pt должна уточняться на основе критерия (4.92).

4.8.3.5. Схоздмость. Традиционный метод сопряженных градиентов сходится в тех же предположениях, что и метод наискорейшего спуска. Для достаточно широкого класса функций теоретическая скорость его сходимости при точной одномерной минимизации оказывается п-шаговой сверхлинейной. Это означает, что

Доказательство п-шаговой сверхлинейной сходимости традиционного метода существенно использует наличие рестартов. Алгоритмы без рестартов для большинства функций сходятся линейно. Однако это - теория, а на практике все выглядит несколько иначе. Наш опыт показывает, что из-за ошибок округления реальная скорость сходимости метода сопряженных градиентов почти всегда линейна независимо от того, применяются рестарты илн нет. Исключения бывают только в очень специальных случаях, например когда минимизируемая функция F(x) представляет собой квадратичную форму с хорошо обусловленной матрицей. Впрочем, это и не суть важно, поскольку при больших п свойство «п-шаговой сверхлинейной сходимости» особой ценности не имеет. Оно не исклю-