
 |
|
Главная Методы условной оптимизации [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [ 49 ] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] Многие из методов решения негладких задач с ограничениями разрабатывались ради конкретных приложений. Обычно эти методы опираются на технику прямого сопоставления значений функций (см. разд. 4.2.1), и поэтому их часто называют методами прямого поиска. В подавляющем большинстве они имеют эвристическую природу и не гарантируют успеха. Некоторые методы прямого поиска работают со штрафными или барьерными функциями (как, например, алгоритм ND из разд. 6.2.2.2). Желающим познак01П1ться с ними палучше мы рекомендуем обзорную статью Свэна (1974). 6.3. МЕТОДЫ ПРИВЕДЕННЫХ ГРАДИЕНТОВ И ПРОЕКЦИЙ ГРАДИЕНТОВ 6.3.1. ОБЩИЕ СООБРАЖЕНИЯ Методы, О которых речь пойдет ниже, получаются обобщением стандартной техники решения задач с линейными ограничениями иа нелинейный случай. Все они далее называются методами типа приведенных градиентов. Эти методы довольно сложны и нередко бывают представлены в таком виде, что за массой алгоритмических деталей усмотреть их суть и принципиальное родство бывает непросто. Мы же начнем с изложения общей основы и только потом перейдем к формальным описаниям. Методы типа приведенных градиентов для задач с нелинейными ограничениями и рассмотренные в гл. 5 методы активного набора воплощают одну и ту же идею: двигаться к решению по допустимым точкам, монотонно уменьшая целевую функцию и сохраняя равенства в некоторых ограничениях (что ведет к сокращению размерности области минимизации). Последнее требует специальных средств, позволяющих постоянно (т. е. в любой пробной точке) согласовывать значения переменных с выдерживаемыми равенствами. Когда ограничения линейны, такое согласование достигается за счет особой конструкции направлений поиска. На нелинейный случай данный подход непосредственно не обобщается. Поэтому для отслеживания изогнутой границы допустимого множества приходится применять итеративные процедуры «коррекции». Проиллюстрируем сказанное на примере двумерной задачи с единственным ограничением вида 5 + x;exp(x;sinu,-x,)) = 0. (6.11) Он задает функциональную связь между Xi и Xj, вси.лу которой одна переменная определяет другую. Таким образом, для минимизации остается только одна степень свободы. Чтобы при известной х, подобрать Хг, обеспечивающую (6.11), надо применить какую-нибудь процедуру поиска нуля типа описанных в разд. 4.1.1. Делать допустимые шаги с уменьшением целевой функции при сохранении ряда равенств можно по-разному. Разными могут быть и правила перебора списков «замораживаемых» на равенствах ограничений. Конкретный набор соответствующих приемов дает конкретный метод типа приведенных градиентов. Раньше термины «проекция градиента» и спрнведеииый градиент» употреблялись в отношении вполне определенных преобразований. Здесь, однако, онн трактуются значительно более свободно и относятся к любому преобразованию «проектирования» F в «приведенное подпространство» точек, удовлетворяющих набору условий-равенств. 6.3.2. ПОИСК ПРИ ОГРАНИЧЕНИЯХ-РАВЕНСТВАХ В ЭТОМ разделе описана итерация метода типа приведенных градиентов при заданном списке фиксируемых на равенствах ограничений (обсуждение вопроса о том, как строить такие списки при решении задач с неравенствами, откладывается до разд. 6.3.3). Через с (X) будем обозначать их /-мерную вектор-функцию, а через Xj-текущее приближение, причем с (х) = 0. Следующим приближением будет точка Xj+i, в которой должны быть выполнены равенство t(Xs+,) = 0 и условие «существенного убывания» f (см. разд. 4.3.2.1). Шаг из х, в х, обозначим через s. 6.3.2.1. Определение составляющей шага в нуль-пространстве градиентов ограничений. Первое, что требуется от искомого шага - это подчинение равенству c(x. + sJ-0. (6.12) Будь вектор-функция с линейной, для конструктивного описания всех подходящих мы воспользонались бы техникой, изложенной в разд. 5.1.1. При нелинейной сэта техника тоже полезна; она позволяет описать первые приближения для Sj. Возьмем линейную аппроксимацию с в окрестности Xj, по Тейлору: с(Х„ + S„) « с (Xj -I- А Ы = /Г (Xj) Sj. (6.13) Из нее видаю, что множество допустимых аппроксимируется подпространством векторов Pi, представляющих собой решения системы линейных уравнений вида Лл = 0, (6.14) где через обозначена матрица А (Xj). Эта система аналогична системе (5.5), определяющей допустимые направления в линейном спучае, но только теперь в си.пу нелинейности ограничений матрица от итерации к итерации будет меняться. По ана.логни с (5.6) можно утверждать, что множество ps, удовлетворяющих (6.14), описывается формулой Р*=4Р2. (6.15) где есть матрица, чьи п-( столбцов формируют базис подпространства векторов, ортогональных строкам \, а р-произвольный (п-/)-мерный вектор. Таким образом, для построения приближений к есть n-t степеней свободы (представленных вектором Pz). Конкретный Pz обычно выбирают так, чтобы обеспечить ми-ни.мум какой-то аппроксимации целевой функции, выраженной через Pz. К примеру, в ранее рассмотренных алгоритмах применялся вектор «наискорейшего спуска» Рг-Це. (6.16) (Отметим, что ZZjgj есть проекция градиента целевой функции F на подпространство векторов, ортогональных градиентам активных ограничений.) Чтобы получить более высокую скорость сходимости, при выборе Pz надо использовать информацию о вторых производных; в частности, Pz можно вычислять как решение уравнения Z?«Ap = -Zfg., (6.17) где -некоторое приближение матрицы Гессе функции Лагранжа. Матрицу Zj определяют по-разному. Расиространеиным способом является метод исключения переменных, представленный в разд. 5.1.3.2. Алгоритмы, в которых он реализован, объединяют под названием «методы обобщенных приведенных градиентов». Напомним, что данный способ построения Z исходит из расчленения на две составляющие, одна из которых невы-рожденная квадратная (х «-матрица. К примеру, если первые ( столбцов линейно независимы, можно расчленить так; 4 (У U). где V невырожденна. Тогда соответствующей Z будет (6.18) При использовании Zj из (6.18) процедура построения pj становится особенно прозрачной. Разобьем, подобно А, вектор р,, на составляющие ру и рц (то же сделаем и с градиентом gj). Условие (6.14) позволяет выразить t «зависимых» переменных ру через n - t «независимых» р, т. е. понижение размерности до n - t может быть реализовано в терминах исходных координат. Это и происходит, когда применякуг матрицы (6.18): в данном случае р совпадает с р. Название «методы обобщенных приведенных градиентов» объясняется тем, что просто методом приведенных градиентов принято называть алгоритм с р = = -UV-gy-gv, т. е. с Pz = -Zlgk, где определяется формулой (6.18). 6.3.2.2. Восстановление допустимости. Если бы ограничения были линейными, шаг нз Хк в Xk-, можно было бы искать в виде уРк, где у - некоторое число, а ps задается формулой (6.15). Однако при нелинейных ограничениях такойдааг, вообще говоря, приведет в недопустимую точку, т. е. использовать Рк как «направление поиска» в обычном понимании этого термина не удается. Стандартная для методов типа приведенных градиентов формула опредстеиття допустимого шага Sj выглядит следующим образом: SkyPk + УкРу. (619 Здесь Yi,-матрица, составленная из векторов базиса ранг-пространства Л. Требование допустимости точки Xj-t-Sj означает, что число у и вектор Ру в (6.19) будут связаны друг с другом. Проще говоря, Ру зависит от у, и, таким образом, подгонка значения у-процедура более сложная, чем обычный одномерный поиск. Как правило, значение у, позволяющее получить допустимый шаг, определяется в итеративном режиме: просматриваются пробные V, для каждого из которых делается попытка решить ( нелинейных уравнений с (Хк -i-s„)c (х„ -Ь урп -Ь УкРу) = О (6-20) относительно ( неизвестных компонент вектора Ру. Поиск ру есть адаптивная подзадача, так как количество обращений к процедурам расчета функций ограничений (и их градиентов), которое потребуется для решения системы (6.20), заранее неизвестно. Эта задача может оказаться дефектной - система (6.20), вообще говоря, будет разрешимой ие для любого у. При естественных предположениях разрешимость (6.20) гарантирована, если значение у достаточно мало. В методах обобщенных приведенных градиентов матрицу строят так: Это значит, что допустн.мость обеспечивается подгонкой вариаций зависимых переменных Xv. (Именно таким способом в предьщущем разделе предлагалось сохранять равенство (6.11).) 6.3.2.3. Уменьшение значения целевой функции. Мало найти пару у и Ру, удовлетворяющую (6.20),- надо подобрать у так, чтобы было выполнено еще и условие «существенного убывания» f (x*-bsj<f (х,)~6., (6.21) где 6ft-некоторая положительная величина (см. разд. 4.3.2.1). В слабых предположениях относительно можно доказать, что среди малых у всегда найдутся подходящие. После того как значение у, обеспечивающее (6.20) и (6.21), получено, в качестве xi берут Xu+Sk, определяют новый вектор pz и т. д. Подводя итоги, можно сказать, что построение шага в методах типа приведенных градиентов предполагает клниейиый» расчет Pz и «нелинейную» подгонку Ру. При этом решается подзадача выбора у, которая адаптивна сама но себе и, кроме того, включает подчиненную адаптивную подзадачу поиска корня системы (6.20). На рис. 6g изображены результаты двух первых итераций метода типа приведенных градиентов для задачи из примера 6.2, едииствениое ограничение которой фиксируется на равенстве. Цифрой О помечено начальное нрибли-жение. Прочими цифрами занумерованы пробные точки метода (в том порядке, в котором они просматривались). Первая и вторая пробные точки в выделенный 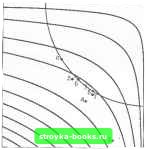 Рис. eg. Точки двух первых итераций метода тнпа приведенных градиентов при решении задачи из примера 6.2 с ограничением, зафиксированным иа равенстве. мент не попали. Значения pz определялись из уравнения (6.17). Точки с номерами 6 и 8 - это два найденных методом допустимых точек приближения с уменьшающимися значениями F. В данном примере получилось так, что первые же значения у, для которых удавалось подобрать ру, удовлетворяли и (6.21). 6.3.2.4. Свойства методов типа приведенных градиентов. Методы приведенных градиентов и проекций градиентов включены во многие библиотеки математического обеспечения и очень неплохо работают для задач, ограничения которых «почти линейны». Если же нелинейность ограничений значительна и начальная точка далека от оптимальной, требование соблюдения равенства (6.20) с высокой точностью может приводить к тому, что продвижение к решению будег осуществляться очень малыми шагами. Дело в том, что, чем больше кривизна допустимой поверхности, тем меньше значения у, позволяющие восстановить допустимость и при этом не растерять выигрыш но критерию, достигнутый шагом из л: в касательном направлении. Методы тина приведенных градиентов имеют тенденцию идти к решению «вдоль границы», и это становится не- достатком, когда она сильно искривлена. Так проявляется неточность линейной анпроксимапин ограничений, положенной в их основу. Чтобы избежать потерь эффективности, связанных с требованием жесткого соблюдения ряда равенств, неоднократно выдвигалось предположение занижать точность их выполнения на промежуточных итерациях. Это, однако, означает отход от основного принципа методов типа приведенных градиентов, т. е. приводит к методам иной категории. Некоторые из них могут быть интерпретированы как методы спроектированного лагранжиана, рассмвтриваемые в разд. 6.5. 6.3.3. ОПРЕДЕЛЕНИЕ РАБОЧЕГО СПИСКА Чтобы применить описанную выше технику для задач с неравенствами, ее надо скомбинировать с какой-нибудь «стратегией активного набора» подобно тому, как это делается в линейных случаях. Здесь есть широкое поле возможностей, но, хотя способы воплощения предлагаемого подхода бывают разными, суть всегда одна: на каждой итерации как-то прогнозируется список активных в решении неравенств н выделенные тем самым ограничения «замораживаются» на равенствах. Отметим отличие от методов барьерных функций (см. разд. 6.2.1.2), в которых все ограничения все время выполняются как неравенства и могут становиться равенствами лишь в пределе. Стратегии активного набора реализуются введением «рабочего списка». Это - перечень ограничений, которые в данный момент трактуются как равенства, причем только они учитываются при выборе Pz и вычислении поправки ру. От итерации к итерации состав рабочего списка может изменяться. Для задач с неравенствами помимо прочего усложняется процедура построения шага s. В частности, подбирая у в (6.19), надо следить за неактивными в начале итерации ограничениями. Если полученное значение у приводит к тому, что какое-то из них нарушается, у надо уменьшить и итеративно подогнать таким образом, чтобы вновь проявившееся ограничение стало равенством (после чего ввести последнее в рабочий список очередной итерации). Центральным местом любой стратегии активного набора является правило вывода ограничений из рабочего списка. Эти правила чаще всего опираются на оценки множителей Лагранжа, которые подробно рассмотрены в разд. 6.6. Критерии целесообразности вывода ограничения и способы вычисления оценок множителей в разных версиях схемы типа приведенных градиентов бывают разными. Иногда в методах типа приведенных градиентов стратегию активного набора реализуют неявно, преобразуя все нелинейные ограничения в равенства введением вспомогательных переменных, подчиняемых условиям неотрицательности. Тогда эти ограничения [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [ 49 ] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] 0.0016 |