
 |
|
Главная Методы условной оптимизации [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [ 58 ] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] конечное множество зиачеинй. В последнем случае найти оптимум, как правило, оказывается намного сложнее, чем в NCP; некоторые подходы к решению задач с дискретными переменными упоминаются в разд. 7.7. Подбирая алгоритм для конкретной задачи типа NCP, обязательно надо принимать во внимание ее специфику. Если она достаточно отчетлива, обращаться к алгоритму, рассчитанному иа самый общий случай, неразумно. Рациональный выбор определяется различными свойствами функций задачи. По некоторым совокупностям этих свойств выделяются классы задач, каждому из которых отвечает своя предпочтительная схема поиска оптимума. Типовая классификация представлена в разд. 1.2. Одни характеристики задачи очень сильно влияют на сложность ее решения, другие - намного слабее. Возьмем, к примеру, размерность. Ее увеличение приводит к разному возрастанию сложности только «в двух точках»: во-первых, при переходе от одномерных задач к многомерным и, во-вторых, когда а) данные задач перестают умещаться в оперативной памятн машины и Ь) для повышения эффективности счета приходится начинать эксплуатировать слабую заполненность (большую долю нулевых элементов) матриц производных. Что же касается «отрезка» между этими «точками», то на нем усилия, требуемые для решения типичной задачи, грубо говоря, зависят от ее размерности как полином умеренной степени. По-это.му, скажем, безусловная минимизация по двенадцати переменньм обычно немногим сложнее, чем по девяти. Совсем иначе отражается иа трудоемкости задачи форма ее условий. Лучше всего, когда их вообще нет или когда все они суть простые ограничения иа переменные. (Надо сказать, что переход от безусловной минимизации к минимизации при простых ограничениях иногда даже ускоряет решение.) Достаточно заменить последние линейными ограничениями общего вида - и поиск оптимума ощутимо усложнится. Появление нелинейных ограничений повысит сложность еще на порядок (см. гл. 6); поэтому иногда, если это возможно, стоит переформу-чировать модель так, чтобы в ней не было нелинейных ограничений (см. разд. 7.4). Среди свойств функций оптимизационной задачи, облегчающих ее решение, самым фундаментальным, по-видимому, является дифференцируемость. Она позволяет эффективно аппроксимировать функции по их локальным характеристикам, и это используется в алгоритмах, К примеру, если существуют непрерывные вторые производные, то локализовать решение намного легче, чем в случае с недиффереицируемыми функциями. Поэтому большинство программ оптимизационного математического обеспечения рассчитано именно на гладкие задачи, и, если можно сформулировать модель в терминах гладких функций, так и надо сделать (см. разд. 7.3). Выбор алгоритма решения гладкой задачи конкретного типа зависит от того, какая информация о производных доступна, насколько велика трудоемкость их вычисления и т. д. При этом общая тенденция такова, что с увеличением объема используемой информации о производных надежность и эффективность алгоритмов возрастают (см. разд. 8.1). 7.3. ИСКЛЮЧЕНИЕ НЕОБЯЗАТЕЛЬНЫХ РАЗРЫВНОСТЕЙ Эпитет «необязательных» в заголовке этого раздела фигурирует потому, что, строго говоря, результаты вычислений с конечной точностью никогда не составят непрерывной функции. К тому же обычное математическое определение непрерывности, включающее произвольные малые приращения функции и ее аргумента, при операциях иад конечным мьюжеством чисел, представимых в формате с плавающей запятой, просто неприменимо. В общем «машинная версия» любой функции разрывна по своей природе. Однако, если сама функция гладкая и хорошо отмасштабирована, эта разрывность несущественна - она не затруднит работы предполагающих гладкость алгоритмов оптимизации; к плохо отмасштабироваиным функциям сказанное ие относится. Проблема масштабирования будет кратко обсуждаться в разд. 7.5 и подробнее - в разд. 8.7. Поскольку задачу с недиффереицируемыми функциями общего вида решать тяжело, при формировании оптимизационной модели их по возможности следует избегать. Другое дело - специальные случаи типа рассмотренных в разд. 4.2.3 и 6.8; с ними трудностей не возникает. Мы хотим подчеркнуть, что важно отличать недиффе-ренцируемые функции от функций, производные которых (по каким-то причинам) недоступны. У первых просто нет производных в некоторых точках; например, у функции шах {Xi, х} нх нет при Xi=Xi. У вторых они есть всюду, и сам факт их существования уже имеет значение для выбора алгоритма. Из сущности модели обычно не так уже трудно понять, дифференцируемы составляющие ее функции или нет. Если у моделируемого процесса есть критические точки, скажем может переполниться какой-то резервуар или допустимо переключение производства с одного ресурса на другой, то разрывы производных возможны. Иначе их скорее всего ие будет. Даже если в отношении диффе-реицируемости ничего определенного сказать нельзя, то обычно для начала стоит предположить, что она есть: неудачная попытка решить задачу методом, рассчитанным на гладкие функции, обойдется не так уже дорого по сравнению с теми усилиями, которые потребуются для ее решения алгоритмом, не предполагающим глад- КОСТИ- 7.3.1. РОЛЬ ТОЧНОСТИ ВЫЧИШЕНИЯ ФУНКЦИЙ МОДЕЛИ На практике нередки оптимизационные задачи, которые не надо решать с высокой точностью (она, например, ни к чему, когда в порождающей задачу модели заведомо не отражены какие-то сущест- вениые свойства исследуемого объекта или ее параметры подобраны по весьма приближенным данным), и бытует заблуждение, что в подобных случаях точно вычислять функции задачи тоже бессмысленно. Считают, что их достаточно оценивать лишь слегка поточнее, чем требуется оценить оптимум. 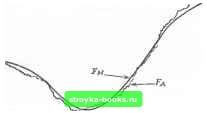 Рис. 7а. Аппроксимация модельной функции Tjm, удовлетворительная в смысле поточечной близости, ио неудобная для метода поиска минимума. Пусть Fu(x) - истинная характеристика некоторого объекта, а Рм(х) - моделирующая ее функция. Заботясь лишь о поточечной близости к Fu(x), значения F„{x) можно вычислять и с ошибками, только бы онн были малыми относительно уклонения Fj, от F. Но отсюда еще не следует, что такне ошибки не помешают методу оптимизации. Если они привнесут в модельную функцию или ее производные существенные разрывы, то эффективность метода скорее всего сильно упадет. Обозначим через а„ относительную погрешность приближения f н с помощью f „. Как правило, истинная величина остается неизвестной и удается получить лишь ее оценку снизу (по точности исходных данных илн по значимости игнорируемых свойств объекта). Коль скоро а„ очень мала, автор модели, конечно, постарается реализовать вычисления с максимальной точностью. Однако чаще Ом лежит в диапазоне 0.1%-5.0%, Допустим, что прн этом есть две вычислимые аппроксимации f скажем F и Fg, уклонения которых от Fm, допускаемые ради облегчения расчетов, не превосходят величины Ос- Если существенно меньше, чем а„ (например, ОсжО.О! %), ТО в смысле близости к f я Функции F и F будут приближениями ТОГО же качества, что и Fm- На рис. 7а и 7Ь рассматриваемая ситуация показана (в несколько утрированном для наглядности варианте) для одномерного случая. Если судить только по уклонениям \Ft,{x)-Fa(x)1 и \Fu{x)-Fii(x)\, изображенные функции F и Fb моделируют f д одинаково хорошо. В то же время для метода минимизации онн совершенно различны. В частности, Рв является гладкой, а у fл и ее производных есть МНОГО разрывов. Последние чреваты целым рядом неприятностей. Прежде всего у Fj есть точки локальных минимумов, далекие от точки минимума F, и поиск вполне может сойтись в какую-то из иих. Трудности иного рода возникают при использовании для минимизации Fa конечно-разностных приближений производных: если 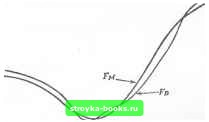 Рис. 7Ь. Гладкая аппроксимация модельной функции Ff. интервал аппроксимации захватит точку разрыва, полученная оценка производной будет негодной, даже когда градиент в текущей точке хорошо определен. Казалось бы, высказанные предостережения должны быть адресованы только узкой аудитории самых непосвященных, поскольку умышленно вводить в модель ненужные разрывы, разумеется, ни1СГ0 не станет. Однако практика показывает, что заблуждение относительно безобидности шалых» неточностей подсчета функций распространено шире, чем можно ожидать. 7.3.2. Аппрокстлция по ряд.\.ч и таблицам По нашему опыту одной из самых частых причин потери гладкости является обращение при расчете модельной функции F(x) к некоторым вспомогательным функциям W(y). Поскольку машины могут выполнять только э.чемеитарные действия, эти функции всегда как-то аппроксимируются- Часто приближениями служат отрезки рядов, выбор которых зависит от аргумента. Таким образом, может, например, случиться, что для оценивания W(y) будут использованы две формулы - одна при малых у, а другая при больших. Граничные у, вообще говоря, оказываются точками разрывов. Даже если W(y) при всех Y аппроксимируется на основе одного ряда, длины выбираемых отрезков для ра.яличных у могут быть разными; скажем, прн Y=4.7 могут использоваться четыре первых члена ряда, а при Т=4.7-Ь10-Ч пять. Чтобы избежать указанных разрывностей (илн по крайней мере свести их последствия к минимуму), рекомендуется (i) по возможности исключать смены формул (например, фиксируя длину отрезка ряда, которым приближается функция); (ii) если смены формул допускаются, ю обеспечивать их стыковку гю значениям генерируемой функции (и, если удается, ее первых производных). К сожалению, прибегая к стандартным программам вычисления вспомогательных функций, пользователь обычно не может контролировать смеиу формул. К примеру, стандартная библиотечная процедура подсчета функции Бесселя /„(у) реализует два метода и переключается с одного на другой при у=11. По этой причине иногда приходится заменять библиотечные программы своими. Еще одни источник иегладкости, схожий по природе с рассмотренным,- применение табличных функций. Допустим, F(x) зависит от величины V (у), затабулированной для набора значений у= =0(0.01)1. Возникает вопрос: как определять V(у) в промежуточ-иых точках? Проще всего брать в качестве У(у) табличное значение из ближайшей к у точки, кратной 0.01. Тогда, например, если требуется величина (0.6243), вместо нее будет использована V(0.62), и в смысле близости к F подобный подход вполне приемлем. Однако фактически это означает замену V (у) кусочно-постоянной функцией, разрывность которой может привести к осложнениям. Линейная интерполяция V(y) между уз-чами сетки дает непрерывную функцию, ио первые производные будут разрывными. Лучшее же (и всегда реализуемое) решение - вообще отказаться от таблиц и заменять их гладкими аппроксимирующими функциями типа сплайнов. Даже дву1.1ериые таблицы удается эффективно представлять гладкими поверхностями. 7.3.3. ОПРЕДЕЛЕНИи ФУНКЦИИ ПОДЗАДАЧЕЙ Более запутанная ситуация возникает, когда значение модельной функции определяется решением некоторой подзадачи, например интегрированием дифференциальных уравнений илн какой-то другой функции. Построение тахого решения с полной машинной точностью (что, кстати сказать, ие всегда возможно) обычно требует значительных усилий. Поэтому, как правило, его считают непозволительной роскошью, имея в виду, что и дифференциальные уравнения, и интеграл, и любая другая математическая конструкция все равно есть лишь приближенное описание чего-то реального Возьмем для примера часто встречающуюся задачу безусловной минимизации по х интеграла (x) = ]f(x, t)dt. (7.1) Аналитически проинтегрировать /(х, t) обычно не удается, и приходится использовать какую-нибудь численную квадратурную схему. Последняя даст вместо истинной величины f (х) ее приближение, равное взвешенной сумме значений / в избранных точках: \ f (X, t)diKiI (t. m) = 2 m,./(X, tj). (7.2) Здесь {coj.} - веса, a {i} - набор абсцисс, удовлетворяющих соотношениям 0<<1<:...<:<м<Ь. Ошибка оценки (7.2) зависит от производных / по < порядка выше первого, числа точек [tj] и их расположения на отрезке [й, Ь]. Наиболее совершенные методы численного интегрирования являются адаптивными. В них tj в (7.2) подбираются по ходу вьгаис-леиий в соответствии с наблюдаемьж поведением /; общий принцип состоит в том, что, чем сложнее ведет себя /, тем «плотнее» надо располагать точки. Есть немало хороших реализаций адаптивных методов, и, коль скоро какая-то из соответствующих программ доступна, естественно возникает желание вычислить F в (7.1) с ее помощью. Однако при минимизации F это чревато теми же неприятными последствиями, что и применение стандартных программ расчета приближений функций по рядам (см. разд. 7.3.2). В силу своей итеративной сущности адаптивная квадратурная схема может выбрать сильно различающиеся наборы {Л-} даже для близких значений X. Это значит, что генерируемое пр бл жен е F будет иметь нежелательные разрывы, хотя его равномерная близость к F гарантируется. Кривая оценок интеграла, вычисленных адаптивным методом, вполне может напоминать с рис. 7а. Следует подчеркнуть, что адаптивное численное интегрирование в рассматриваемом случае непригодно только потому, что по рай-ией мере вдали от решения) гладкость аппроксимации F здеь важнее, чем ее точность. При поиске минимума (7.1) лучше пользоваться квадратурными формулами с фиксированными (соу) и [t]. Они определяют гладкие фуигщии /. Подав на вход метода минимизации такую /, мы получим точку X, как-то приближающую х*. Скорее всего х недостаточно хорошо оценит х*, и поэтому надо выполнить еще один шаг - применить более надежную квадратурную формулу (скажем, с увеличенным, но по-прежнему фиксированным числом точек М) и повторить минимизацию, взяв х в качестве начального приближения. Если /(х, t) - достаточно хорошая фунхщия, разумный выбор абсцисс позволит получить улучшенную оценку минимума F при умеренном увеличении их числа. Кроме того, так как х все же неплохое приближение х*, много раз подсчитывать / для повторной минимизации не придется. В результате будет найдена точная оценка х*, и, если нужна не только она, ио и точная оценка величины F(x*), в завершение всей процедуры можно один раз вычислить интеграл [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [ 58 ] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] 0.0019 |