
 |
|
Главная Методы условной оптимизации [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [ 60 ] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] Если преобразование дает возможность снять не все, а только некоторые нелинейные ограничения, то скорее всею прибегать к нему не стоит. Однако нет правила без исключений; сказанное не относится к большим задачам, для которых ценой каких-то замен удается автоматически удовлетворить условиям, включанхаим много переменных, и тем самым добиться, чтобы матрица Якоби функций ограничений стала разреженной. 7.4.2. ЗАДАЧИ С ФУНКЦИОНАЛЬНЫМИ ПЕРЕМЕННЫМИ Важный класс оптимизационных задач, непосредственно не вписывающихся в конечномерную постановку задачи NCP, образуют задачи поиска экстремума на функциональных множествах. Например, может потребоваться найти минимум интеграла lf(x(t),t)dt (7.11) на пространстве гладких функций x(t) аргумента ( из отрезка [а, Ь\. Во многих случаях подобные задачи удается «сводить» к конечномерным; принцип соответствующих преобразований мы проиллюстрируем на (7.11). Чтобы обрабатывать на машине функции х((), их надо представлять конечными наборами данных, причем ясно, что хранить значения x{t) в огромном числе всех машинно-представимых точек отрезка определения нереально. Значит, нужен С1Юсоб генерирования удовлетворительного приближения x(t) по информации разумного объема. Последнюю можно интерпретировать как определение новой функции х(0, получающейся какой-то интерполяцией x(t) в незатабулированных точках. Близость х к х будет зависеть от гладкости X и X, числа и расположения точек интерполяции и т. д. Итак, под удовлетворительным решением задачи миннмизапни интеграла (7.11) будем понимать некую функцию x(t). Пусть все х строятся в виде -(0 = .Е с,-ш,(о. (7.12) v*S? Р - комплект так называемых базис- ных функции; в качестве часто используют (i) степенные функции -М Л •о Чебышева; u,,=T, S); (iii) В-сплайны: щ= -M,(t) Тогда, подставив правую часть (7.12) вместо х в (7 111 мы приходим к конечномерной задаче с неизвестными {сЛ В зависимости от структуры / интеграл (7.11) либо можно буде\ шять аналитически, либо при каждом наборе {с,) придется оценивать численно (соображения по поводу использования численных мегодов интегпи рования приведены в разд. 7.3.3). ин1ири Замечания и избранная библиография к разделу 7.4 Детальный анвлиз квадратичной замены переменных проведен Снссером (1981). Использование кусочнополиномиальной интерполяции для решения (квадратичных) функциональных задач очень подробно обсугадается в работе Сьярле, Шульца и Варги (1967); см. также Гилл и Мюррей (1973а). Определения полиномов Чебышева и В-сплайнов даны, например, у Кокса (1977). 7.5. МАСШТАБИРОВАНИЕ Есть ряд давно осознанных вычислительных проблем, говоря о которых неизменно употребляют термин «масштабирование». Тем не менее четкого определения этого термина нет. Поэтому не удивительно, что с масштабированием связано немало путаницы и что в публикациях его стараются не касаться. В данном разделе мы обсудим лишь простые замены переменных и специальный прием масштабирования для нелинейных задач о наименьших квадратах. Более подробно вопросы масштабирования рассмотрены в разд. 8.7. Там даны рекомендации как для задач на безусловный экстремум, так и для задвч с ограничениями. 7.5.1. МАСШТАБИРОВАНИЕ ЗАМЕНОЙ ПЕРЕМЕННЫХ Масштабирование заменой переменной состоит в переходе от первичных единиц измерения, обычно отражающих физическую суть задачи, к новым, более подходящим для метода ее решения. Этот прием не следует смешивать с преобразованиями, которые обсуждались в разд. 7-4.1 и изменяли тип задачи. Первая основная цель масштабирования - добиться, чтобы в представляющей интерес области модули значений преобразованных переменных имели одинаковые порядки. Дело в том, что в оптимизирующих программах допуски на нарушения условий экстремума в правилах останова и другие критерии по необходимости используют неявные определения понятий «мало», «много» и, когда из-за большого разброса модулей переменных этн определения утрачивают универсальность, возлюжны осложнения. Возьмем, к примеру, задачу (оптимизации теплообменника), некоторые из переменных которой перечислены с указанием единиц измерения и характерных значений в табл. 7а. Последние имеют сильно различающиеся порядки, и в этом нет ничего удивительного, так как рассматриваются разные физические величины. Из сопо. ставления третьего н четвертого чисел видно, что большой разброс могут иметь и переменные одинаковой размерности. Как правило, для масгцтабирования следует применять линейные замены переменных (хотя иногда допустимы и нелинейные). Чаще всего обращаются к заменам вида где {Xj} - исходные переменные, {у} - преобразованные, D - диагональная матрица. В качестве ее диагональных элементов используют характерные значения модулей соответствующих переменных. Для задачи, к которой относится табл. 7а, при таком подходе di надо взять равным 1.1x10*. Таблица 7а. Характерные значения иеотмасштабнрованных переменных
к сожалению, указанное преобразование иногда может приводить к специфическим потерям точности. Допустим, например, что исходная переменная х,- должна лежать в диапазоне 1200.1242, 200.1806]. Тогда, масштабируя ее «ио характерному значению» 200.1242, для преобразованной переменной получим диапазон, который с точностью до семи значащих цифр равен 11.0, 1.000282]. Если мантисса представления числа па машине содержит семь десятичных разрядов, именно это приближение будет использовано в вычислениях. В нем область допустимых значений новой переменной У] отражена с точностью до трех значащих цифр В то же Время диапазон для Xj представим без погрешностей. Масштабирование диагональным преобразованием ненадежно и тогда, когда в процессе минимизации модули переменных существенно изменяются. В этом случае те dj, которые естественно взять в одной точке, могут совершенно не годиться в другой. Если известен вероятный диапазон значений переменной, обе упомянутые выше трудности преодолеваются одним приемом. Допустим, каким-то образом установлено, что х,- в течении всей процедуры решения задачи будет удовлетворять неравенствам 0/х> Тогда новую переменную у/ можно ввести по формуле в матричных обозначениях (7.17) записывается так: x=Dy+c, где D - диагональная матрица, чей /-й диагональный элемент равен 4Jp,-aD, ас - вектор, составленный из полусумм U{a,+h,). Гарантировано, что, какова бы ни была величина Xj из [Cj, bj\, отвечающее ей в силу (7.18) значение У) не выйдет из диапазона -1 У/-Ы- В описанном вып1е примере с потерей точности формула (7.17) принимает следующий вид: Xj=O.02824/j-f200.1524. При этом диапа.зон для у,, соответствующий отрезку [200.1242, 200.1806], представляется ограничениями -l<i <-f 1 без погрешностей. Мы хотим подчеркнуть, что преобразование (7.17) применимо, только если известны хорошие приближения крайних значений Xj. Имея лишь очень грубые оценки последних (т. е. оценки, возможно отличающиеся от настоящих границ на несколько порядков), использовать его нельзя ни в коем случае. При переходе от х к у по формуле (7.18) наряду с переменными масштабируются и производные. Пусть g, С и g, G„ - градиенты и матрицы Гессе до и после преобразования соответственно. Тогда gy=Dg, Gy=DCD. Отсюда видно, что даже «умеренные» изменения масштабов переменных типа xlOz/; сильно отражаются иа вторых производных и потому могут существенно влиять на скорость сходимости оптимизационного процесса. 7.5.2. МАСШТАБИРОВАНИЕ В НЕЛИНЕЙНЫХ ЗАДАЧАХ О НАИМЕНЬШИХ КВАДРАТАХ Нелинейные задачи о наименьших квадратах чаще всего возникают, когда нужно подобрать вектор параметров х модельной футшции у{х, (), обеспечивающей наилучшее совпадение ее значений в выделенных точках [tj] с наблюдаемыми в них значениями {ijj} реальной величины, зависимость которой от t моделируется. Методы решения задач данного класса обсуждались в разд. 4.7. Многие задачи о наименьших квадратах характерны тем, что масштабы их переменных автоматически определяются выбором масштаба независимой величины t. Как это происходит, мы покажем на примере упрощенной формулировки некоторой реальной задачи (сохранив ее специфические обозначения). Эта формулировка звучит так: требуется подобрать параметры {Л;}, /=0, .... У, и {Вд, Ph, Oj), k=\, .... К, функции yip)- (7. IS) обеспечивающие минимум суммы (7.18) где величины {К,} и {Ау,} фиксированы. Речь идет о настройке на данные эксперимента комбинации К гауссовых кривых и полиномиального фона (первого слагаемого в правой части (7.19)) Опорные точки и результаты подгонки параметров (7.19) при К=4 показаны ?56б*57бГ "" координат пиков) лежат в диапазоне 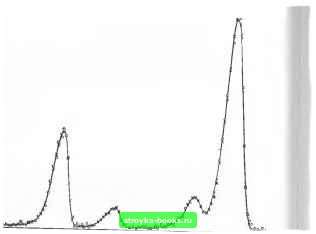 560 576 Рис. 7с. Результат подгонки параметров гладкой функции под данные наблюдений; параметры получены решением нелинейной задачи о наименьших квадратах. При решении поставленной задачи без предварительного масштабирования неизбежны большие трудности, так как даже для умеренных / коэффициенты при Л, оказываются огромными и соответственно оптимальные Aj должны получаться очень близкими к нулю. Скажем, при /-3 переменная Аз в каждой компоненте у (pi) минимизируемой суммы умножается на число, нижней оценкой которого служит 566=й;10*. Проблема частично снимается, если заменить Pi на Zi, связанные с Pi формулой р=57&г. Тогда модули новых Aj будут больше модулей старых в 576 раз. Однако при таком изменении масштаба независимой величины р, как и в случае, разобранном в предадущем разделе, неоправданно теряется точность представления диапазона ее значений. Чтобы этого не произо- ) лучше воспользоваться преобразованием р=52+571, при ко-,м все Zi также ложатся на отрезок [-1, --11. В преобразованной задаче место у{р) займет функция Ф (г) = t i Вк exp . После того как оптимальные {Aj], и {а) найдены, решение исходной задачи (т. е. оптимальные {Aj\, и {о для функции (7.19)) вычисляется по несложным формулам. Впрочем, если сами по себе {А\, \р\ и {гу\ не нужны, такие вычисления не понадобятся, поскольку значения функции у{р) можно (и лучше) определять по Ф (г) на основании равенства у1р) = Ф((р-571),5). 7.6. ПОСТАНОВКА ОГРАНИЧЕНИЙ 7.6.1. ВЫРОЖДЕНИЕ Неудачная формулировка модели с ограничениями на переменные может привести к плохо поставленной оптимизационной задаче даже тогда, когда, по существу, решение хорошо определено. Многообразие совершаемых оплошностей такого сорта довольно обширно и даже слишком обширно, чтобы перечислять их в этой книге. К примеру, нередко вводят избыточные ограничения, которые представимы линейными комбинациями основных и предназначаются только для того, чтобы заставить алгоритм автоматически вычислять какие-то сводные показатели. Пользователь знает, что решение от этогоне изменится, и полагает, что на процессе поиска это тоже не отразится. Однако данное предположение оправдывается далеко не всегда. Часто неприятности возникают, когда между переменными задачи и характеристиками изучаемого явления иет прямого соответствия. Это положение мы проиллюстрируем примером из собственной практики. Рассматривалась статистическая модель заболеваемости раком легких. Основой исходного описания служили трехиндекс-ныевероятности {pijk}, i-1, /=1, J. k=\, ..., К, и ми- нимизируемая функция зависела только от них. При обсуждении одной из постановок было решено выражать [рцц] произведениями трех двухиндексных вероятностей, т. е. пользоваться представлением Pijk=fugtkh,k. (7.20) Для {gjh) и {hik) удалось выписать разумные ограничения, и тем самым была поставлена нелинейная задача на условный экстремум с {ftj}, {gn), {h,h] в качестве переменных. Некорректность постановки вскрылась после того, как в численных экспериментах выявились систематически серьезные за- [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [ 60 ] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] 0.0015 |