
 |
|
Главная Микрокалькулятор [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [ 34 ] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] сними функциями. Например, sh X chx = th л; и -г- = cth X. chx ~ " sh X Гиперболические функции задаются соотноше ниями shx-chx--thx: cth X - e 2 При больших значениях x член e- очень мал, поэтому значения гиперболических функций можно вычислять по приближенным формулам sh л: PS ch х = th л: cth X I (при д:= 10 погрешность при замене точных формул приближенными составляет Л/ е""). Гиперболический косинус известен в технике под названием цепной линии - такую форму принимает цепь или тяжелая гибкая нить, подвешенная за концы (рис. 9). При этом безразлично, идет ли речь о жемчужном ожерелье, свисающем с шеи женщины, или о трансатлантическом кабеле, провисшем над расселиной в дне океана. Существует еще одна важная гиперболическая функция thx. Она известна, как «функция роста». При больших по абсолютной величине положительных и отрицательных значениях х гиперболический тангенс стремится снизу и сверху к двум асимптотам (последнее означает, что зазор между гиперболическим тангенсом и этими прямыми становится сколь угодно узким), параллельным оси х и проходящим через точку у = +1 и г/ = -1 оси у (рис. 10). Гиперболический тангенс возникает в различного рода расчетах, связанных с прогнозированием процессов с насыщением. Такие процессы встречаются довольно часто. Прирост численности ученых в стране или сбыт телевизоров, кухонных щкафов и стиральных мащин достаточно хорощо описываются гиперболическим тангенсом. Отличительные особенности такого процесса заключаются в том, что сначала развитие 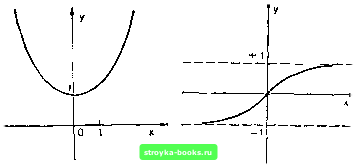 Рис. 9. Цепная линия. Рис. 10. Гиперболический тангенс. Асимптоты показаны пунктиром. его происходит совсем медленно (техническая новизна, высокая цена, несоверщенство конструкции), затем темп стремительно возрастает (предмет широкого потребления, массовое производство, совершенная конструкция) и, наконец, наступает насыщение (обычно одной семье не требуется более одного телевизора или автомашины). Для прогнозирования удобно пользоваться гиперболическим тангенсом, записанным в виде где X - время, 5 - постоянная насыщения, С - время «полунасыщения» и k - еще один параметр. Состояние исследуемого объекта в момент времени X характеризуется величиной у. Если произведено достаточно много измерений (х,-, у с), то можно определить постоянные S, С ш k (см. раздел «Линейная регрессия»), и специалист, занимающийся составле-лением прогноза, получает возможность, исходя из положения дел, в один момент времени предсказать ожидаемые значения величины у в будущем. При вычислении значений гиперболических функций воспользуемся испытанным методом, пригодным для микрокалькуляторов (см. раздел «Математическая «хитрость»). Для получения приближенной формулы оборвем степенной ряд на третьем члене chx=i++4+ После несложных преобразований получаем y = chx---. Схема вычислений выглядит следующим образом: Сжатие Растяжение Хо у о = Ch Хо й-кратное деление Ui-i = 2г/, - 1 пополам (4+зУ-з х„ « 0,3) -> --= у„ Относительная ошибка меньше Ю"*. По известному значению y = chx значения других гиперболических функций нетрудно вычислить по формулам cth д: = [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [ 34 ] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] 0.0009 |