
 |
|
Главная Микрокалькулятор [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [ 48 ] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] МО удержать 6 членов. Чем больше интересующее нас значение z, тем длиннее отрезок степенного ряда требуется для достижения заданной точности, то есть тем более громоздкой становится формула для вычисления P{z). Это обстоятельство не давало покоя математикам до тех пор, пока они не нашли для P{z) следующее приближение, годное для больших Z (при г = 2 погрешность составляет около 2 % от точного значения); Подставляя z= 1,5, получаем; Р(1,5) 1---7==-= 0,9137 « 91,4 %, 1,0 у ля что соответствует 2-8,6 = 17,2% брака. При столь малых значениях z отклонения от истинного значения достигают уже около 20 %, но в качестве первого приближения названной вами оценки было бы предостаточно. Приемлема ли для заказчика такая доля брака или необходимо создать новый токарный станок (позволяющий обтачивать валы с меньшим разбросом s вокруг среднего значения м), не в силах решить ни вы сами, ни обратившийся к вам контролер ОТК. Но вы подготовили рациональное обоснование для принятия решения, произведя ясный и убедительный расчет. КАК ИЗВЛЕКАТЬ КОРНИ В извлечении квадратных корней нашими духовными праотцами были древние вавилоняне. Они пользовались приближенной формулой Последуем их примеру: разложим подкоренное выражение (то, что стоит под корнем) на полный квадрат и остаток и вычислим приближенное значение квадратного корня при помощи приближенной формулы, стоящей в правой части равенства. Вот как это будет выглядеть: V40" = 6 + - 6,33 (более точное значение: 6,324553). Более точные приближения мы получим, если воспользуемся методом, разработанным великим естествоиспытателем Исааком Ньютоном, но восходящим еще к Герону Александрийскому (около 100 г. н. э.). Пусть Ul - первое приближение к значению квадратного корня . Следующее, улучшенное приближение 02 мы найдем по формуле а если потребуется более высокая точность, то третье, четвертое и т. д. приблиления вычислим по аналогичной формуле an+i = j("«+i) "Р п = 2, 3, 4..... Последовательные приближения «шаг за шагом» к точному значению, осуществляемые по однотипным формулам, называются итерациями. Воспользуемся методом Ньютона для вычисления л/40. В качестве первого приближения (так как д/36 = 0, а /49 -7) выберем ai = 6,5. Вычисляя, получаем последовательные приближения а2 = у (6,5 + -) «. 6,327, ЙЗ = J (6,327 + ) - 6,32458, «4 = (6,32456 -f) 6,324553. Сравнив их с приведенным выше точным значением, мы убеждаемся в том, что три итерации позволяют получить пять верных знаков после запятой. В ходе вычислений вы можете сэконо.мить операции, если очередное приближение будете сохранять в регистре: ведь именно оно послужит начальным значением при вычислении следующего приближения Если у вашего микрокалькулятора имеется клавиша для вычисления квадратного корня, то необходимость в методе вычисления квадратных корней, разумеется, отпадает, хотя при желании вы можете самостоятельно оценить достижения вавилонских математиков. В связи с извлечением корней нам бы хотелось продемонстрировать один нехитрый трюк. Если вам 1 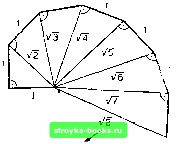 ИТ д. Рис. 18. Графический способ извлечения квадратного корня из натуральных чисел. понадобилось вычислить выражение вида V+o и в памяти микрокалькулятора нет места для хранения промежуточных результатов и Ь, то, выполнив несложное преобразование вы сможете проделать все выкладки, не прибегая к записи промежуточных результатов. Теорема Пифагора позволяет извлекать квадратные корни из целых чисел «чисто геометрически» (рис. !8). Извлечение квадратного корня представляет собой не более, чем частный случай извлечения корней л-й степени из числа. Аналогично этому приведенная выше итерационная формула Ньютона является не чем иным, как частным случаем общей формулы - га- 1 (га - 1)а [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [ 48 ] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] 0.0009 |