задан в мм. Выберем шарик диаметром 5 мм. Нагрузка F составляет

F = 30- 52 = 750 кгс.

Из выражения для Яб видно, что пресловутый здравый смысл не позволяет нам высказать какие-либо утверждения относительно различий в свойствах двух марок сталей. Разумеется, у вдвое более твердой стали величина Нб вдвое больше. Но твердость по Брпнеллю Яб мы вычисляем, а измерить нам удается лишь диаметр отпечатка d. Лишь d позволяет судить о свойствах той или иной марки стали.

Чтобы разобраться с твердостью до конца, произведем на иашем микрокалькуляторе два расчета; сначала вычислим диаметр отпечатков шарика для обеих марок стали при

Яб, = 2Яб„

а затем твердость каждой из марок по Бринеллю при

= 0,51

(если марка 2 тверже марки 1, то диаметр отечатка d2 должен быть меньше диаметра отпечатка di).

Предположим, что более мягкая сталь имеет твердость по Бринеллю, равную 120 кгс/мм. В первом случае (Яв, = 2Яб,) твердость по Бринеллю марки 2 равна 240 кгс/мм Чтобы вычислить диаметр отпечатка d, преобразуем выражение для Яб следующим образом:

Яб =

nD-(D- - )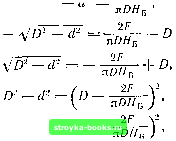

При Яб = 120 кгс/мм получаем di = 2,7l мм. При удвоенном значении Яб2 = 240 кгс/мм диаметр отпечатка оказывается равным di = 1,95 мм. С увеличением твердости по Бринеллю диаметр отпечатка, как и следует ожидать, уменьшается.

Вычислим теперь твердость по Бринеллю для случая, когда диаметр отпечатка d шарика в стали одной марки вдвое меньше, чем в стали другой марки. Будем исходить из диаметра отпечатка d==2,71 мм. Твердость по Бринеллю в этом случае нам известназ Яб = 120 кгс/мм. При d = 2,71/2 мм получаем

„ 2F

ПБ,-

nD {D ~ л/п ~ ) 2-750

= 510 кгс/.мм

Вычислить значение последней дроби можно различными способами. Лишь немногие микрокалькуляторы позволяют производить вычисление дробей «с листа», то есть находить сначала числитель, а затем знаменатель: для этого требуется располагать несколькими регистрами памяти и стеками.

Обычно вычисления удобно начинать с d. Если у вашего микрокалькулятора имеется кла-

виша

то вы можете воспользоваться

ею, чтобы произвести все выкладки в обратном порядке (вычислить сначала знаменатель и лишь затем числитель). Обратите внимание на

то, что £>2 2 2 JD2

Итак, при уменьшении диаметра отпечатка d вдвое твердость по Бринеллю Яб возрастает более чем вчетверо: со 120 кгс/мм до 510 кгс/мм, и мы на собственном опыте убеждаемся, насколько трудно составить интуитивное представление о твердости. Лишь быстродействие микрокалькулятора позволяет во всех случаях получать численные значения интере-. сующих нас характеристик материалов.

дни РОЖДЕНИЯ И ЛОТЕРЕИ

В нашей книге «Seltsames um den gesunden Men-schenverstand» («Когда здравый смысл заблуждается») мы предлагаем читателю такую задачу: «В классе учатся 40 мальчиков и девочек. Какова вероятность того, что по крайней мере у двоих из 40 учеников дни рождения совпадают?»

Многие сочтут правильным следующий ход рассуждений. В году 365 дней. Если исключить влияние на рождаемость празднеств и погодных условий, а также двадцать девятое февраля, то в среднем через каждые 9 дней кто-нибудь из 40 школьников будет отмечать день рождения. Поэтому вероятность совпадения двух дней рождения ничтожно мала. Сколь ни разумным кажется такое «решение», оно в корне неверно. Ошибка заключается в необоснованном смешении средних и вероятностей. В своей книге мы приводим формулу

гуг 365-364- ... • (365-ra-f 1) Vn- 365»

где Wn - вероятность того, что в произвольной по составу группе из п человек ни у одной пары дни рождения не совпадают. Совпадение двух дней рождения из данных п служит событием, дополнительным к первому, поэтому 1 - Не так давно мы бы могли написать: «Еще никому не удавалось вычислить W при я = 40». Теперь высказать такое утверждение было бы непростительным легкомыслием.

Если у вашего микрокалькулятора имеется клави-

то именно она и поможет вам произвести

необходимые вычисления. Попробуйте найти вероятности Wn для начала по крайней мере до п = 25. Предположим, что ваш микрокалькулятор представляет большие числа в виде степеней десятки от 10" до 10+ (именно в этих пределах работает большинство микрокалькуляторов). Тогда, ио формулы для Wn при п = 25 вы получите:

Г25 «4,92-1063; 1,14-10* = 0,43,