мем за следующее приблил<ение к х:

X, - Х2

X г» Ха = Хо - у, •

Рассмотрим пример. Предположим, что требуется найти нуль уравнения

/ (;с) = Х2 - 1П X - 2 = 0.

Методом проб и ошибок находим:

/(1) = 1<-0,

/(2)= 1,307 >0.

Следовательно, нуль уравнения, который мы хотим найти, заключен между хо = 1 и xi == 2 (при этом

Рис. 19. Метод хорд. Секущие позволяют зажать корень х в сколь угодно узкую вилку.

г/о = -1, а г/1 = +1,307). Проведя хорду через точки Ро и Рь получаем:

= - = 2 - 1.307 . = 1.433

г/2 = (1,433)2 In 1,433 2 == -0,305.

Так как при Xi < х всегда будут получаться лишь отрицательные значения функции yi, то конец хорды, совпадающий с точкой Pi.(xb yi), остается непо-

движным, в то время как координаты другого конца изменяются шаг за шагом:

3 - X. - у, f = 2 - 1,307 1 о7+о!зо5 - Ь541;

t/з = -0,058;

д:4= 1,560; 1/4 = -0,010;

д:д= 1,564; 2/5 = -0,002.

На этом мы можем остановиться, так как Хб дает приближенное значение нуля хс тремя верными знаками после запятой.

МОРСКИЕ И ВОЗДУШНЫЕ ПУТИ

Суда дальнего плавания и самолеты трансконтинентальных линий следуют из пункта отправления в пункт назначения по кратчайшим маршрутам.

На поверхности земного шара кратчайшее расстояние между любыми двумя точками совпадает с длиной дуги большого круга, соединяющей эти две точки. Напомним, что большим называется круг, центр которого совпадает с центром шара, в нашем случае -с центром Земли (рис. 20).

Экватор ограничивает большой круг, меридианы, идущие от полюса к полюсу, также являются дугами больших кругов, а вот линии равной широты не принадлежат к числу дуг больших кругов. Остальные дуги больших кругов, соединяющие пары точек на поверхности Земли, в северном полушарии обращены выпуклостью на север. Следуя из Москвы в Нью-Йорк кратчайшим маршрутом, мы по дороге приблизимся к Северному полюсу. Этим и объясняется интерес авиационных штурманов к полярным маршрутам.

Сколь велико расстояние от Берлина (ф = 52°25 северной широты, Я = 13°30 восточной долготы) до Гаваны (ф = 23°15 северной широты, = 82°30 западной долготы) по дуге большого круга? (Географические координаты аэродромов в Берлине и в Гаване мы указываем приближенно, чтобы упростить

последующие расчеты.) Географические координаты Берлина как пункта отправления мы пометим индек-со.м о, географические координаты Гаваны как пункта назначения - буквой н.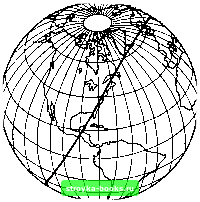

Рис. 20. Кратчайший путь (ортодромия). На поверхности земного шара кратчайший путь между любыми двумя точками проходит по дуге большого круга.

Длина L дуги большого круга, соединяющей две точки на поверхности земного шара, определяется выражением

L = 60

arccos sin [фо • sin ф„ -j-

+ cos Фо • cos фн • COS (Ян - Яо)],

где арккосинус измеряется в градусах.

До появления микрокалькуляторов это соотношение наводило ужас на навигаторов: чтобы вычислить L, им приходилось по 6 раз заглядывать в таблицы тригонометрических функций и интерполировать табличные значения синусов, косинусов и арккосинуса. Ясно, что процедура была не только утомительной, но и приводила к большим погрешностям.

Прежде чем поручить нашему микрокалькулятору работу высококвалифицированного штурмана, служащего на флоте или в авиации, необходимо сделать следующие замечания.