раз и фаза сдвинулась на jx/2. Следовательно, коэффициент передачи идеализированного тракта

/„(io)) = sin(na)/a,o)e-""/"° :zz!!»e"°+" (2:4)

где то - постоянное время задержки, которое всегда возникает э реальных цепях.

Типичный вид коэффициента передачи идеализированного тракта приведен на рис. 2.4. При со=0 /С(ю)=0, что естественно, так как, если даже в сердечнике головки будет создан постоянный по уровню магнитный поток, он не сможет навести ЭДС в обмотке индукционной головки. Дальнейший рост частоты ведет к увеличению модуля коэффициента передачи со скоростью 6 дБ/октаву (в 2 раза при увеличении частоты также в 2 раза) Такой закон возрастания /С(со) наблюдается в той области частот, которой сооТ-ветствуют большие длины волн сигнала и соответственно практическое отсутствие волновых потерь. Пропорциональное возрастание уровня сигнала при увеличении частоты является следствиег дифференцирования магнитного потока при создании ЭДС индукционной головкой. г «

При дальнейшем увеличении частоты начинает сказываться* пРпяГ""""Р" уменьшающих модуль коэффициента пе й2пр„,?°пУ° ™™- РУ-ьтате одновременного влияние* St?t.nTP° Tf воспроизводящей головки и волно а .ятрТ1 """ коэффициента передачи достигает максимума» ?ительно /-««ьшаться. Максимум смешен влево отно

Ko~xTLolL--у-у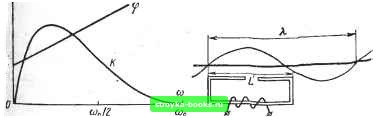

Рис. 2.4. Амплитудно-частот- Рис. 2.5. Воспроизведение си

ная и фазово-частотная харак- нала, длина волны которог

теристики тракта воспроизве- сравнима с длиной раб

поверхности головки

дения

абочей

Фазовая характеристика линейна. Ее наклон определяется bI менем задержки то. Начальный фазовый сдвиг на п/2 вызван Д» Фереицирующим действием воспроизводящей головки и оПрД ет ()азовые искажения сигнала. дО-

Проведенный анализ идеализированного тракта является аточно простым и приводит к компактным аналитическим ° от ниям отдельных составляющих коэффициента передачи.

анализ основан-на принятой простой аппроксимации функции чув. ствительности воспроизводящей головки. Существуют более стро, гие, хотя и значительно более сложные способы расчета волновые потерь, в частности использование метода взаимности и конфорц. ных преобразований. Оказалось, что и при этом выражения длд контактных и слойных потерь совпадают с полученными выще; что касается коэффициента щелевых потерь, то он, хотя и описы!. вается гораздо более громоздким выражением, чем функция sin xjx, в рабочей области частот мало отличается от полученного, выше коэффициента Ке, при условии увеличения геометрической ширины рабочего зазора примерно на 10%. Это расчетное значе-ние ширины рабочего зазора называется эффективным, т. е.

(2б)эфф=1.1 X 2 6. (2.5)

При расчете амплитудно-волновых характеристик тракта в выражение для щелевых потерь следует подставлять значение эффективной ширины рабочего зазора.

При рассмотрении идеализированной модели тракта воспроизведения исходили из нескольких допущений. В последующих параграфах этой главы будет рассмотрено, к каким дополнительным искажениям амплитудно-волновых характеристик приводит отказ от этих допущений.

2.3. ВЛИЯНИЕ НА АМПЛИТУДНО-ВОЛНОВУЮ ХАРАКТЕРИСТИКУ КОНЕЧНЫХ РАЗМЕРОВ ГОЛОВКИ

Допустим, что головка воспроизведения, имеющая конечную длину рабочей поверхности, равную L, воспроизводит гармонический сигнал и длина волны записи сравнима с длиной рабочей поверхности головки (рис. 2.5). В этом случае магнитный поток носителя попадает в сердечник головки не только в области рабочего зазора, но и по всей длине L. Среднее значение этого потока определяется интегрированием по длине рабочей поверхности:

вр =

T-.J

sin 2я- dx =

Фо1 - со5 2л;-j.

(2.6)

Из выражения видно, что среднее значение потока периодически изменяется и поэтому амплитудно-волновая характеристика в области больших длин волн имеет нерегулярный характер. Кроме того, при LIk=Q Фср=0. Это означает,

Рис. 2.6. Амплитудно-частотная характеристика тракта с учетом неравномерности в обла-сти низких частот • "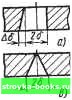

Рис. 2.7. Типичные дефекты рабочих зазоров головок

отличие от характеристики, показанной иа рис. 2.3г, характеристика ре-что головки при значении 1Д=0 проходит через начало координат (рис. 2.6) "оэтому волновой коэффициент передачи при воспроизведении постоянной на-и "„ценности равен нулю. Физический смысл этого обстоятельства состоит в что намагниченный однородно по длине носитель записи не создает потока "ссеяния и поэтому такая намагниченность воспроизведена быть не может. Колебательный характер амплитудно-волновой характеристики определяет явление аналогичных колебаний у амплитудно-частотной характеристики в области низких частот. Такие колебания АЧХ называют иногда «змейкой».

2 4 ВЛИЯНИЕ НА АМПЛИТУДНО-ВОЛНОВУЮ ЗАРАКТЕРИСТИКУ ДЕФЕКТОВ РАБОЧЕГО ЗАЗОРА

Рассмотрим, как влияют на амплитудно-волновую характеристику тракта воспроизведения некоторые дефекты рабочего зазора. При этом надо иметь в виду, что рассматриваемые дефекты не означают, что головка непригодна для использования. Будем интересоваться не грубыми дефектами, появление кото-рь1х достаточно для отбраковки головки, а только теми из иих, которые неизбежно возникают при массовом производстве и связаны с наличием технологических допусков на точность изготовления. Возникающий из-за наличия таких дефектов разброс характеристик определяет тот диапазон, в пределах которого система коррекции АЧХ тракта должна иметь запас регулировки.

Возможны следующие основные дефекты рабочего зазора.

Непараллельность граней. Возникает из-за неточности сборки. Типичные дефекты этого вида показаны на рис. 2.7. Для вычисления амплитудно-волновых характеристик головок с такими зазорами можно воспользоваться выражением (2.1), положив в нем для упрощения a=d=Q, что будет соответствовать контактному воспроизведению с бесконечно тонкого носителя. Отличие амплитудио-волиовой характеристики от коэффициента щелевых потерь идеализированной головки определит ее искажения из-за дефектов рабочего зазора. Из выражения (2.1) при a=d=G имеем для гармонического потока ленты Фг(л:) =OocosQx:

с» с»

<D(x)= т](ОФИ/ -д:)й/=ФоСС8Йх jT)(/)ccsQZd/-f

- 00 -ов

rf©eSinfix jT](OsinQ/rf/ = OoBiCCsQA;-f ФоВаБШЙх, (2.7)

У головки с симметричным рабочим зазором функция ri(/) - четная и второй интеграл в выражении (2.7) равен нулю, так как он определяет интегрирование четной функции в симметричных относительно нуля пределах. При несимметричных зазорах функция чувствительности головок не обладает четностью. Поэтому оба интеграла не равны нулю и

Ф {X) = ф„ /Сд (й) COS (Qx- фд), (2.8)

где 95=arctg(Bi/B2) - фаза коэффициента волновых потерь; Кд(Й) =

VВ\-\-В2 - модуль коэффициента волновых потерь.

Таким образом; при наличии дефектов у рабочих зазоров кроме изменения Модуля коэффициента волновых потерь появляется и дополнительный фазовый сдвиг, зависящий от длины волны. Если этот фазовый сдвиг не пропорционален волновой плотности записи Й=2л;/Я, то возникают фазовые искажения. Расчеты для изображенных на рис. 2.7 зазоров дают следующие резуль-

рис.2 7а- J!£M±AS/4) . ......

*~ ft(6-fA6/4) • COS fl 6 - cos fl (6 + A6/2) (sin flA6/2)/(flA6/2) -• sinfl6-f sinfl(6-f AS/2)(einflA6/2)/(flA6/2)