вычисляется отношение контурных размеров пьезоэлемента к ег( толщине.

Относительное изменение частоты пьезоэлементов в выбран, ном интервале температур (ТКЧ). Кроме геометрических размеров пьезоэлемента, определяющих его частоту, необходимо полу, чить ряд других данных, имеющих большое значение для работы кварцевых резонаторов. В первую очередь надо найти минималь-ные значения ТКЧ прн выбранной рабочей температуре. Изменение ТКЧ в довольно широких пределах достлт-ается изменением угла среза пьезоэлемента. На рис. 2.1 показаны кривые ТКЧ для разных рабочих температур круглых пьезоэлементов среза yxll+ 35° в зависимости от изменения угла среза. Из кривых ви,;-но, что нулевой ТКЧ можно получить при рабочей температу -1-20°С, вырезав пьезоэлемент среза ух1 под углом 35°10.

7ИЧ xfO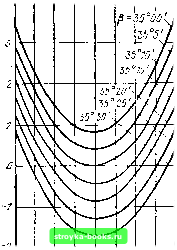

SD-ifO~w с го 0 60 tic

Рис. 2.1. Зависимости ТКЧ пьезоэлементов среза yxll+ 35° от температуры и угла среза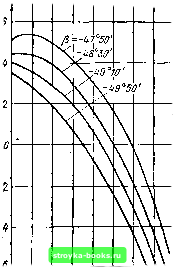

-SO-W-ZQ а го 40 е.о t,°c

Рис. 2.2. Зависимости ТКЧ пьезоэлементов среза yxll-49° от температуры и угла среза

На рпс. 2.2 даны кривые значений ТКЧ для разных рабочи температур круглых пьезоэлементов среза yxll-49° в зависимости от изменения угла среза. По прямой, вычерченной на рис. 2.3 в других обозначениях координатных осейт можно найти точку нулевого ТКЧ для заданной температуры, -выбирая соответственно угол среза пьезоэлемента. На рис. 2.4 и 2.5 изображены частотно-температурные характеристики для пьеэоэлементов срезоА yxll+ 35° п ух -49°.

На рис. 2.4 приведены кривые для круглого пьезоэлемента ср за ух11 + 35° с частотой основного колебания 1000 кГц. Семейств

вых показывает зависимость относительного изменения часто-Af/f пьезоэлемента от температуры окружающей среды и угла ofj То же показано на рис. 2.5 для пьезоэлемента среза / 49° с частотой основного колебания 2000 кГц.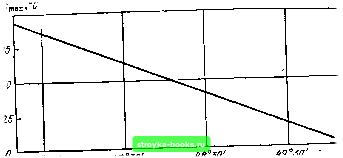

Увал среза

Рис. 2.3. График нулевого ТКЧ среза i/xV-49° в зависимости от угла среза при

разных температурах

На рис. 2.6 представлены кривые для выбора минимального относительного изменения частоты Af/f при оптимальном угле ориентации пьезоэлемента среза yxll+ 35° в заданном интервале температур {At=t2~ti). Закономерность приведенных кривых сохраняется также для линз.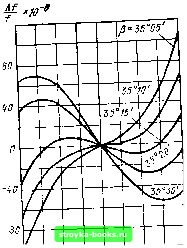

-60 -40 -гп о

го м 60 t,°c

-so-40 -го о го 40 во t,"

Рис. 2.4. Температурно-частот-ная характеристика пьезоэлементов среза yxll+35" в зависимости от угла среза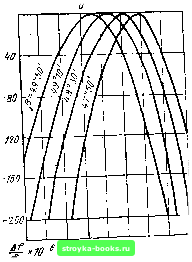

Рис. 2.5. Температурно-частот-ная характеристика пьезоэлементов среза (/xf/-49° в зависимости от угла среза

Срез yxU+35° может быть использован как на сравнительно низких (400 кГц), так и на высоких (100 МГц и выше) частотах. При этом срез yxll+ 35° имеет малую зависимость частоты от температуры в широком интервале температур (см. рис. 2.4). Дл.ч этого среза суммарный уход частоты при изменении температуру от -55 до + 105°С может составить ±20- IQ- [40].

Частотно-температурная характеристика среза ух1/ + 25° пол--ностью определяется ориентацией кварцевой пластины относительно кристаллографических осей. Для небольших интервалов температур ориентация пластин этого среза может быть выбрана таким-, образом, что изменение частоты будет еще меньше. ]

Практически трудно установить точку перегиба характеристика! среза yxll+ 35°. В этом отношении лучше применить срез ухЦ-49°/ так как частотно-температурная характеристика этого среза имеет форму параболы (см. рис. 1.33), приче.м точка перегиба этой параболы регулируется углом среза с большой точностью (рис. 2.5). -

При иопользовании самых тонких пьезоэлементов можно применить срез ух1/-49°, который дает возможность получить пра той же толщине более высокую частоту, так как частотный коэффициент этого среза примерно в полтора раза больше частотного коэффициента среза yx + 35°.

ff<? so m 1Z0

m f.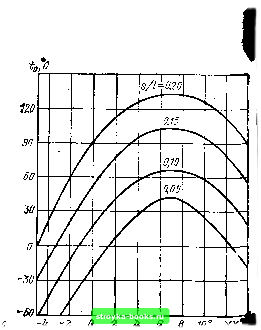

Рис. 2.6. Характеристики относительного изменения частоты пьезоэлементов среза Х( /-Ь35° при оптимальной ориентации для заданного интервала температур

Рис. 2.7. Зависимость нулевого ТКЧ рабочей температуры я выбранного угла среза пьезоэлемента

2.3. МЕТОДИКА РАСЧЕТА ПЬЕЗОЭЛЕМЕНТОВ СРЕЗА xys/+5°, ИМЕЮЩИХ ФОРМУ БРУСКА

Кварцевые резонаторы с брусковыми пьезоэлементами обычно попользуются в низкочастотном диапазоне. Для расчета необходимо в первую очередь определить угол среза пьезоэлемента, при котором получится минимальное значение ухода частоты с "изменением температуры на ГС (ТКЧ кварцевого резонатора), а также найти геометрические размеры пьезоэлемента, определяющие собственную частоту его колебаний (s - толщина по оси X; / - длина по оси У). По кривым, изображенным на рис. 2.7, .можно определить значение рабочей температуры пьезоэлемента для получения нулевого или близкого к нулевому ТКЧ в зави-симости от выбранного угла среза для разных геометри- ШО ческих размеров брусков. Кривые построены для наи- 0 более часто встречающихся отношений 5 = 0,05; 0,10; " 0,15; 0,20.

Из рис. 2.7 видно, что вершины всех кривых соот- 57 ветствуют углу среза, равно- му -1-7°. Для брусков с отно- 5Ш шением s = 0,10 нулевой ТКЧ можно получить при температуре -f60°C (наиболее удобная температура Off-термостатированйя кварцевого резонатора) и при угле среза -f4°30. Изменение угла среза от 6 до 7° будет меньше всего влиять на значение ТКЧ.

На рис. 2.8 представлена о зависимость частотного коэффициента Nf от отноше- ШО-

ния размеров s и угла сре-

за. Для расчета пьезоэлемен- р„с. 2.8. Зависимость частотного коэффи-тов задаются собственная циента от отношения s/l я угла среза частота, интервал рабочих

температур, в котором предполагается использование кварцевых резонаторов, и желаемое среднее значение ТКЧ в этом интервале.

Пьезоэлементы рассчитываются с помощью кривых рис. 2.7 и 2.8. Частота пьезоэлемента при колебаниях изгиба

flfs Nf S . /2 / /

5200 5100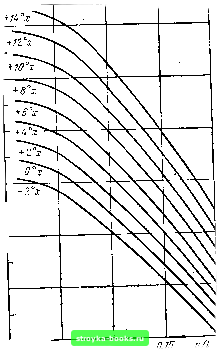

Отсюда видно, что частота, геометрические размеры пьезоэлеме тов, частотный коэффициент и ТКЧ связаны между со-бой,.

На практике можно пользоваться нрйближенным эмнирич! ским графиком (рис. 2.9), тогда расчет пьезоэлементон упрощае ся. По этому графику, показывающему связь частоты пьезоэлеме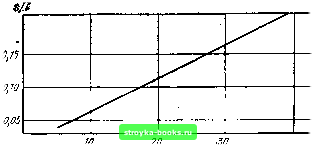

Рис. 2.9: Приб женный график для расчета гео-метрических раз-меров пьезоэлементов

та с его геометрическими размерами, получаем численное знач ние отношения s/l. Зная отношение s/l, выбираем угол среза т., кнм, чтобы средний ТКЧ в рабочем интервале температур ,был минимальным. По значениям s/l и углу среза находим по графику (рис. 2.8) значение частотного коэффициента, после чег,о можно рассчитать размеры пьезоэлемента. Приведем пример расчета.

1ребуется рассчитать пьезоэлемент иа частоту 15 кГц с рабочей температурой термостата +60° С.

По графику рис. 2.9 находим отношение s/l, равное 0,09, для частоты 15 кГц. Зная это отношение и температуру" =60° С, по графику рис. 2.7 определяем угол среза пьезоэлемента, равный -Ь4°30, затем по графику рис 2 находим значение частотного коэффициента-Л = 5580.

Рассчитываем размеры: ,,

ЛГ/ S 5580 /

-0,09 = 33,48 мм;

/ 15

5=0,09 г = 0,09.33,48 = 3,01 мм.

Мы определили длину "Ги толщину s бруска. Ширина b е данном случае может быть выбрана такой, чтобы сечение бруска было близким к квадрату, т. e.fc = 3,0 мм. Размеры пьезоэлемента равны 33,48X3,01x3,0 мм. Проверяем значение частоты пьезоэлемента этих размеров:

, iVfS 5580-3,or что, близко к заданному.

2.4. МЕТОДИКА РАСЧЕТА ПЬЕЗОЭЛЕМЕНТОВ ДВОЯКОВЫПУКЛОГО И ПЛОСКОВЫПУКЛОГО ПРОФИЛЯ СРЕЗОВ ух11 + ЗЪ° и yxll-49°

В настоящее время плоские пьезоэлементы срезов yxl/+ 35° yxll-49° на частотах ниже 8 МГц все чаще заменяются двояко- я плосковыпуклыми линзами, „обладающими меньшими размерами 72

И более высокой добротностью. У линз амплитуда колебаний уменьшается к краям, что в значительной степени освобождает колеблющуюся систему от системы крепления. Плосковыпуклая форма пьезоэлемента упрощает процесс обработки пластины.

В работе [53] описывается метод расчета низкочастотных кварцевых резонаторов среза yxl/+ 35° в диапазоне частот 80- 3000 кГц (двояковыпуклого профиля) и 1400-3000 кГц (плосковыпуклого профиля). Там же приводятся графики, позволяющие выбрать примерные значения диаметра и радиуса сферы в зависимости от частоты пьезоэлемента.

Расчет двояковыпуклых линз среза yxl/+ 35° приведен также в работе [29], где он сводится к выбору радиуса кривизны R и апределению толщины t по заданным частоте и диаметру d. +j

Радиус кривизны R линзы выбирается по размеру кварнедержателя, куда предполагается установить линзу. Если рассчитываемая линза устанавливается в баллон с наружным диаметром 19 мм, можно рекомендовать следующие значения радиуса кривизны и диаметра d для частот в диапазоне 1000-5000 кГц: = 30-250 мм и rf=il5,5-13 мм. Линзы, показанные на рис. 2.10, с максимальным диаметром d не изготовляются, так как у них будет механически повреждаемый непрочный край. Линзы имеют истинный диаметр d, несколько меньший d. (На рис. 2.10 R - радиус кривизны линзы; t - максимальная толщина линзы; d - диаметр линзы).

Выбрав радиус кривизны линзы, приступают к расчету ее толщины. Толщину линзы t определяют рядом приближенных вычислений. По данным, имеющимся для любой линзы, изготовленной на частоту, близкую

к заданной, находят частотный коэффициент Nf, причем радиус кривизны R линзы должен быть таким же, как выбранный для рассчитываемой линзы.

В табл. 2.1 приводятся данные для нескольких типов линз.

Таблица 2.1

Рис. 2.10. Обозначения размеров двояковыпуклой линзы