
 |
|
Главная Линейные элементы [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [ 11 ] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] 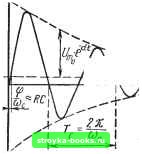 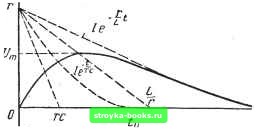 0,Wlr\- 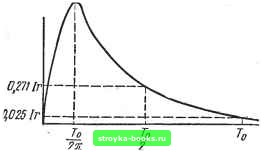 Рис. 1.24 увеличению расходуемой в нем энергии и, следовательно, к более быстрому затуханию колебаний. Последнее подтверждается выражениями (1.33) и (1.35). Помимо колебательного режима, при ударном возбуждении контура на практике встречается апериодический режим. Он возникает при выполнении неравенства а>(Оо. (1.37) Для получения апериодического режима контур обычно шунтируется достаточно малым сопротивлением г. При этом коэффициент затухания а в основном определяется этим сопротивлением, а величиной собственных потерь контура можно пренебречь. Тогда условие (1.37) можно переписать в виде > . или г < - 1/ - . 21 Ylc . ч \ с Для случая, когда г < ]/L/C,дифференциальное ур-ние (1.34) при пренебрежении величиной R имеет следующее решение для и: u{t) 1г\& /- - е cj. (1.38) Как следует из рассмотрения временной диаграммы, построенной на рис. 1.246 в соответствии с ф-лой (1.38), напряжение u{t) представляет собой односторонний всплеск, являющийся разностью двух экспонент, из которых одна обладает малой постоянной времени гС, а другая - относительно большой - L/r. Амплитуда апериодического импульса напряжения Um на контуре оказывается несколько меньше величины Ir. При этом чем сильнее неравенство г <С ]/L/C, тем величина гС, очевидно, меньше значения Ljr и, следовательно, амплитуда Dm оказывается ближе к величине Ir. Длительность апериодического импульса определяется, как это следует из рис. 1.246, постоянной времени L/r и может, как обычно, считаться равной 3L/r. Важно отметить, что увеличение г при неизменных значениях L и С приводит к сокращению длительности импульса. При этом наиболее короткий односторонний всплеск напряжения на контуре будет в случае критического режима ( = J j/- ) • Решение ур-ния (1.34) для критического режима (при пренебрежении, как и раньше, величиной R) имеет вид Из рассмотрения временной диаграммы для критического режима (рис. 1.24 в) следует, что амплитуда импульса Длительность фронта фи и длительность /и всего импульса, измеренная на уровне 3% от амплитуды, соответственно равны: Го = 2я yiC (1.40) 1.6. ЛИНИИ ЗАДЕРЖКИ Линией задержки (ЛЗ) называют линейный четырехполюсник, на выходе которого входной сигнал воспроизводится с задержкой на определенный промежуток времени ts (рис. 1.25й,б).
Рис. 1.25 Для неискаженной передачи сигнала необходимо, чтобы ЛЗ обладала идеальными частотными характеристиками в полосе частот, занимаемой спектром сигнала, т. е. равномерной амплитудно-частотной характеристикой /<(сй) = const и линейной фазо-частот-ной характеристикой ф(ю) = зю. Наклон фазо-частотной характеристики - = 3 определяет время задержки линии. Для неискаженной передачи сигнала произвольной формы, в том числе перепадов напряжения и коротких импульсов с крутыми фронтами, ЛЗ должна обладать идеальными частотными характеристиками во всей бесконечной полосе частот. Однако цепи с такими идеальными характеристиками физически неосуществимы. Поэтому на практике требуют, чтобы характеристики ЛЗ в полосе частот, где сосредоточен основной спектр передаваемого сигнала, были более или менее близки к идеальным. Основными характеристиками ЛЗ является величина и стабильность времени задержки U, искажения формы передаваемого сигнала и объем, занимаемый ЛЗ. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [ 11 ] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] 0.0012 |
||||||||||||||