
 |
|
Главная Линейные элементы [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [ 159 ] [160] [161] [162] где Uj - напряжение на емкости Cj (или ток в индуктивности Lj) е - внешние сигналы, напряжения и токи внешних источников, действующих в эквивалентной схеме. Для линейной схемы система ур-ний (П.8) записывается в матричной нормальной форме (П.9> где и - вектор-столбец независимых переменных, Е - вектор-столбец сигналов, Л и - матрицы коэффициентов. 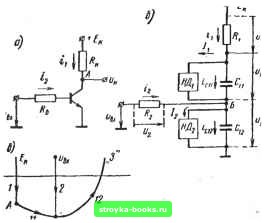 Рис. п.2 Если искомые выходные параметры схемы не совпадают с переменными состояния, то ур-ние (П.9) дополняется матричным уравнением связи Y = CU-f£E, (П. 10) где CnD - матрицы коэффициентов связи. Заметим, что система ур-ний (П.8) [или (П.9) и (П.10)] может быть использована не только для анализа переходных процессов, но и для анализа статических режимов, если рассматривать последние как предельные для переходных режимов (при »со) или если положить в этих уравнениях dujldt = 0 (т. е.. положить равными нулю токи через емкости и напряжения на ин-дуктивностях). Рассмотрим пример составления уравнений в нормальной, форме. На рис. П.2й, б приведены принципиальная и эквивалентная схемы транзисторного ключа; здесь Си и Сц - емкости коллекторного и эмиттерного переходов, Ri = Rh, /?2 == /?б -Ь Гб, hah - токи нелинейных двухполюсников, соответственно коллекторного и эмиттерного переходов. Запишем dUi2 = *2(«II,Ml2) (П.И) r.2 1 *2(«11. «12)=-=7Г-.(12-/2+М) • L-12 l>2 £1 - Mil - «12 »1 «1 jRi 2 /==/l(«n), /2 = /2(«12) (П.Иа) П.4. АВТОМАТИЗАЦИЯ СОСТАВЛЕНИЯ МОДЕЛЕЙ Рассмотрим один способ автоматизации составления уравнений для переменных состояния, основанный на использовании графов 138]. На основе графа электронной цепи записываются ее топологические матрицы, используемые далее для автоматического составления модели. Здесь под графом понимают топологическую структуру (схему), состоящую из вершин (узлов), соединенных направленными ребрами. При исследовании электронной цепи граф топологически отображает ее эквивалентную схему, т. е. узлы и ветви электрической схемы отображаются узлами и ребрами графа (узлами могут также быть шина питания, шина «земля», шина подачи входных сигналов; для упрощения чертежа эти узлы обычно располагаются выше некоторой горизонтальной линии, причем явно на чертеж не наносятся, а на концах ребер, идущих к названным узлам, указываются их обозначения). Обозначения и направления ребер графа соответствуют обозначениям и выбранным направлениям токов (и напряжений источников) ветвей эквивалентнойсхемы. Для удобства различения сопротивления обозначаются числами от 1 до 9 (или от 1 до 99), емкости - от 10 до 19 (или от 100 до 199) и т. д. В качестве примера на рис. П.2б построен граф транзисторного ключа; на рис. П.З приведены другая схема ключа и соответствующие ей эквивалентная схема (в которой опущены нелинейные двухполюсники) и граф. Совокупность ребер, которая включает в себя все узлы графа, но не содержит ни одного замкнутого контура [цикла), называется деревом, эти ребра называются ветвями дерева и выделяются на графе жирными линиями (см. рис. П.2б, ПЗб). Ветви, не вошедшие в дерево, называются главными ветвями (хордами); если в схеме р узлов и q ветвей, то число главных ветвей графа равно q-{p-\). Деревья могут быть выбраны на графе различными способами. Неправильным размещением называют такое, когда в случае графа RC-ixeim в число ветвей дерева попадает одна или несколько резистивных ветвей (неправильное резистивное размещение) или когда в :число главных ветвей попадает одна или несколько емкостных ветвей (неправильное емкостное размещение) Например, в дереве на графе рис. П.2в нет неправильных размещений, а в дереве на графе рис. П.Зе одно неправильное размен щение -резистивная ветвь 3 оказалась в дереве. а) б) чаи. Б- Б Рис. П.З При выборе дерева следует стремиться к тому, чтобы неправильных размещений не было или чтобы их было по возможности меньше, так как при этом упрощаются дальнейшие вычисления. На основе графа и выбранного дерева составляется М-матри-ца - матрица замкнутых состояний. В этой матрице п столбцов (по количеству ветвей дерева и источников питания) и пг cipoK (по количеству главных ветвей). При подключении любой i-й главной ветви к дереву образуется цикл (замкнутый контур). На пересечении строки (Л/-матри-цы), имеющей номер i подключаемой главной ветви, со столбцами, номера которых соответствуют номерам ветвей, входящих в образованный цикл, ставятся цифры 1 или 0: цифра 1 - если направление главной ветви совпадает с направлением ветви дерева, цифра О - в противном случае. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [ 159 ] [160] [161] [162] 0.0014 |
||||||||||||||