
 |
|
Главная Линейные элементы [0] [1] [2] [ 3 ] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] всегда можно определить известными методами теории линейных цепей (методами законов Кирхгофа, контурных токов, эквивалентного генератора и т. п.). С учетом (1.5) ф-ла (1.4) принимает вид д:() = х(оо) +Ле Положив здесь = О, найдем А перепишем теперь в форме x(0) -x(oo). Формулу (1.4) x{t) = x(сю) -f- \х(0) - X(оо)] е (1.6) Таким образом, если в цепи 1-го порядка действуют лишь источники постоянного напряжения (тока), то можно записать выражение x{t) для любого x(t)i переходного напряжения (тока) в цепи согласно ф-ле (1.6), предварительно определив начальное х(0) и установившееся л:(схз) значения и постоянную времени цепи т, что, как правило, не вызывает никаких затруднений. Определим теперь интервал времени = t" - t, в течение которого экспоненциально изменяющаяся функция x{t) (напряжение, ток) возрастает (или убывает) от уровня x{f) до уровня x{t") (рис. Согласно ф-ле (1.6) x{t) -х{оо)-\.{х(оо)~ x{iS)\t , откуда * -1., д;(оо) -x(0) , л;(оо)-л;(0) x(oo)-Ar(V) • аналогично Г = т1п \J ltu-s • Следовательно, 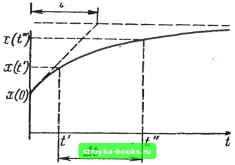 Рис. 1.1 (1.7) Этой формулой будем широко пользоваться при определении длительностей импульсов, фронтов и различных временных интервалов. В качестве примера найдем длительность установления напряжения (тока), изменяющегося по экспоненциальному закону от начального л;(0) до установившегося Jc(oo) уровня. Если выбрать, как условились, 5-процентные уровни отсчета, то x{t) х(0) + 0№[х(оо) - х{0)]; x(t") = x(Q)+ + 0,95[х(оо) х(0)] и согласно ф-ле (1.7) , 0.95 = о;о5 Если приняты 10-процентные уровни отсчета, то ?ф « т In « 2,2т. В дальнейшем принято (если не оговорено другое), что длительность установления экспоненциально изменяющегося напряжения (тока) равна утроенному значению постоянной вреыеик т. 1.3. RC- и RL- ЦЕПИ 1.3.1. МЕТОДЫ РАССМОТРЕНИЯ При изучении импульсных устройств часто рассматривают цепи, представляющие собой простейшие комбинации резисторов и конденсаторов или резисторов и о) катушек индуктивностей {RC- и RL-neneu). Эти цепи применяются непосредственно для формирования импульсов, а также являются важнейшими элементами релаксационных генераторов, триггеров и других устройств. Поэтому рассмотрим основные свойства

Рис 1.2 Рис. 1.3 элементарных RC- и L-цепей и некоторые вопросы, связанные с изменением формы импульсов при прохождении через эти цепи. Отметим, что основные типы импульсов практически можно представить в виде суммы элементарных (типовых) напряжений трех форм: скачкообразного, линейно изменяющегося и экспоненциального (рис. 1.2а,б,в). На рис. 1.3, 1.4, 1.5 приведены примеры замены импульсов прямоугольной и трапецеидальной форм суммами указанных элементарных напряжений. При этом каждое из элементарных напряжений действует от момента его включения (f, Г и т. д.) до =сх5. В спра- .. • ведливости замены легко убе- fl диться, сложив элементарные напряжения (ывхь Wbx2 и т. д.) на каждом из рисунков. Заметим, что при помощи указанных элементарных напряжений обычно аппроксимируют импульсы практически любой j уи/, i j /«в формы. Учитывая сделанное замечание и имея в виду, что рассматриваемые цепи являются линейными, целесообразно для решения интересующей нас задачи воспользоваться принципом наложения. Для этого необходимо после разбивки входного напряжения Ывх(0 на элементарные составляющие I«Bxi(0; Wax 2(О и т. д.] определить форму элементарных напряже-ний на выходе [ubixi{t)\ «вых2(О и т. д.] и далее на основании
 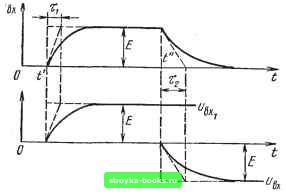 Рис. 1.5 принципа наложения получить выходное напряжение «вых (О в виде суммы Wsbix (t) = «вых 1 (О + «вых 2 (О + • Таким образом, для определения выходного напряжения по заданному входному необходимо, в первую очередь, знать реакции Простейших RC- и RL-цепей на элементарные напряжения. [0] [1] [2] [ 3 ] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] 0.0012 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||