
 |
|
Главная Линейные элементы [0] [1] [2] [3] [4] [5] [ 6 ] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] близка К прямоугольной, амплитуда равна Exlt вх. длительность фронтов - Зт, а длительность импульсов - сумме /фвх + Зт. При увеличении т амплитуда и длительность фронтов выходных импуль- 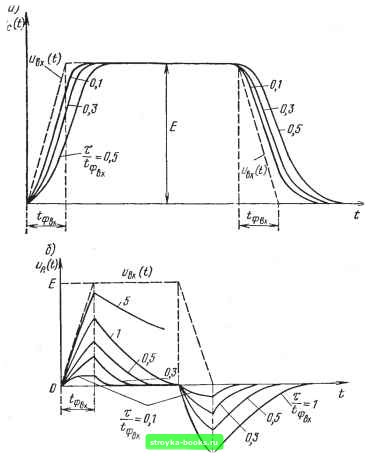 Рис. 1.13 сов Ын(0 растут и при т > О.Зфвх их форма становится пилообразной. При очень больших значениях т(т фвх) форма напряжения Ыл(0 приближается к форме Ывх(0- 1.3.4. РАЗДЕЛИТЕЛЬНЫЕ «С-ЦЕПИ Цепь, изображенная на рис. 1.14а, не пропускает постоянной составляющей напряжения и поэтому называется разделительной. Нестациоадрный процесс в рассматриваемой цепи, возникающий. после подключения к ее входу источника напряжения, проиллюстрирован выше на примере воздействия напряжения прямоугольной формы. При других формах входного напряжения нестационарный процесс носит аналогичный характер и через определенное число периодов после момента включения входного напряжения наступает динамическое равновесие. При этом приращение напряжения на емкости за время ее заряда равно спаду напряжения за время разряда. В таком стационарном режиме постоянная составляющая тока через емкость всегда равна нулю. В силу этого напряжение на сопротивлении, являющееся здесь выходным напряжением Ивых(0. не содержит постоянной составляющей. Естественно, что постоянная составляющая напряжения на емкости в
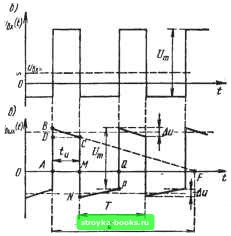 Рис. 1.14 стационарном режиме оказывается равной постоянной составляющей входного напряжения Ывх=- Идеальная разделительная цепь не должна пропускать постоянную составляющую, а переменная составляющая выходного напряжения «вых должна быть в точности равна переменной составляющей входного напряжения Ывх- Переменная составляющая Напряжения на емкости должна быть равна при этом нулю, т. е. Напряжение Uc должно быть равно Ывх = Равенство uc = «вх = выполняется, если в течение одного периода не наблюдается заметного заряда или разряда емкости. Для этого необходимо выбрать Постоянную времени разделительной RC-пепи, значительно превышающую длительность заряда или разряда емкости. Невыполнение этого условия приведет к появлению на емкости заметной переменной составляющей напряжения, а напряжение Нвых(0 скажется при этом искаженным по отношению к Ывх(0- В наиболее важном случае прохождения через разделительную цепь импульсов напряжения прямоугольной формы (1.146) будут наблюдаться искажения в виде завала вершины импульсов. Количественно искажения оценивают относительной величиной g завала вершины прямоугольного импульса напряжения (рис. 1.14в). Под величиной g понимают отношение абсолютного значения изменения Д« выходного напряжения за время заряда или разряда емкости к амплитуде импульса Um = Au/Um- Для определения значения g учтем, что вершина импульса представляет собой практически линейный участок ВС экспоненты. Из подобия треугольников ABF и DBC (рис. 1.14в) следует, что BD/AB = tJx. (1.14) Кроме того, учтем, что площади положительной и отрицательной частей Кривой Ывых(0 равны друг другу, так как постоянная составляющая (среднее значение за период) выходного напряжения равна нулю. Приравнивая площади трапеций АВСМ и MNPQ, получаем АВ ±МС. MN + PQ , Учитывая, что при малой величине завала (АВ -МС)12 ж АВ, {MN+PQ)l2ivUm - AB, получаем {AB)tu {Um - AB)X{T- tvi), откуда ABU{l-tJT). (1.15) Подставляя значение АВ из ф-лы (1.15) в (1.14) и учитывая, что BD равно Ды, находим величину g: При малых значениях коэффициента заполнения y-<g;lj S-„/t. (1.17) Из этой формулы следует, что для получения относительного завала вершины меньше 17о необходимо выбрать постоянную времени разделительной цепи т, по крайней мере, в 100 раз больше длительности импульса. 1.3.5. УКОРАЧИВАЮЩИЕ (ДИФФЕРЕНЦИРУЮЩИЕ) ЦЕПИ Одним из основных применений /?С-цепи является укорочение (или, как часто говорят, дифференцирование) импульсов. Пусть на вход такой цепи с постоянной времени т <С ивх(т = /?С) подан импульс прямоугольной формы (рис. 1.15а). Тогда, как указывалось выше, на выходе (на резисторе) получим два импульса остроконечной формы и чередующейся полярности, начала которых совпадают во времени с перепадами входного напряжения; амплитуда выходных импульсов равна величине Е перепада входного напряже- [0] [1] [2] [3] [4] [5] [ 6 ] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] 0.0014 |