
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [ 108 ] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 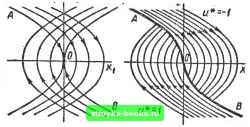 Рис. 10.4 И если вначале и* = 1, то переключение должно произойти на полутраектории OA, уравнение которой получается из первого соотношения при Cl = 0: х + 2л:,=0. Фазовый портрет оптимальной системы показан иа рис. 10.4, б. Уравнение линии переключения АОВ можно записать так (оно легко получается из уравнений для полутраекторий АО и ОВ): х -2x, sign Х2=0, или а(х) = (х1/2) sign Хг-Xi = 0. Нетрудно проверить, что функция о (х) отрицательна справа от линии переключения, где ы* = - 1, а положительна слева, где «•=1, поэтому и* = sign (х sign xj2 - xJ. Реализовать этот закон управления можно посредством устройства, схема которого приведена иа рис. 10.5. В его состав входят нелинейный преобразователь Пр, вырабатывающий совместно с усилителем К значение Хщ = х\ sign х/г, сравнивающее устройство, формулирующее разность е = Хщ - х, и поляризованное реле, иа выходе которого получается оптимальное управляющее воздействие и*. Объект I щ иа схеме представлен двумя инте- р -щ- граторами (1/р). Теперь рассмотрим, как происходит движение изображающей точки при алгоритме управления ы = sign а (х), и поясним, каким образом в п-мерном пространстве при наличии лишь одной (п - 1)-мерной гиперповерхности переключения о (х)=0 получается процесс, состоящий из п интервалов. В случае идеального оптимального процесса 1х* (О, м* (01 все пере- и» I- sign ключения знака управления и* (t) происходят на гиперповерхности о (х) = О, причем после первого переключения изображающая точка идеального оптимального процесса движется по гиперповерхности переключения. Естественно, алгоритм управления и = sign а (х) не может обеспечить такой процесс. Реальный процесс 1х (/), и (/)], определяемый этим алгоритмом протекает следующим образом. В момент /i, когда изображающая точка идеального оптимального процесса в первый раз попадает на гиперповерхность о (х) = О и управление и* {{) меняет знак, изображающая точка х реального процесса «протыкает» гиперповерхность переключения и в момент t = tl + At {At> О, Д/-бесконечно малая величина) оказывается по другую сторону гиперповерхности. Поэтому функция о (х) и управление и (i) меняют знак. Дальше до следующего момента переключения знака управления и (t) изображающая точка х движется по «другой» стороне гиперповерхности вблизи траектории х* (/) идеального процесса. И лишь каждый раз в момент, когда управление и (t) меняет знак, точка х «протыкает» гиперповерхность переключения и функция а (х) и соответственно управление и (t) меняют знак. Поэтому в реальном процессе 1х (t), и {t)] управление и {t) имеет столько переключений (интервалов постоянства знака), сколько и идеальное оптимальное управление и* it). Синтез оптимальных линейных систем по интегральному квадратичному критерию Рассмотрим задачу синтеза оптимальной системы при условии, что объект описывается уравнением i (0=А (О X [t) -f В (О U (О + h (О (10.120) и критерий оптимальности имеет вид J=x4t,)Fx{tj)+jlxt)Qit)x(t) + о -f u(0R(/)u(01. (10.121) Здесь h (f) - известная вектор-функция; F и Q(t) - неотрицательно-определенные матрицы (xFx > О и x"Qx > О при всех х О и / € fо. t/1); R (t) - положительно-определенная матрица (uRu > О при всех х О и t И, tf]). функции А (/), В (t), h (t), Q (О и R (t) являются непрерывными на интервале Ito, tf). Требуется найти управление с обратной связью, при котором при произвольном начальном .условии X (ta) = х" функционал (10.121) принимает минимальное значение. К такой постановке сводится задача управления, если (10.120) является уравнением в отклонениях и соответственнр желаемым является нулевое состояние. Первое слагаемое в (10.121), представляющее квадратичную терминальную.ошибку, включается, если необходимо обеспечить максимальную близость состояния системы в конечный момент времени к желаемому состоянию. Слагаемое \x(t)Q(t)\(t)dt является интегральной квадратической ошибкой и характеризует качество регулирования на всем интервале [/<,, 1-И наконец, интеграл jV(/)R(Ou(OA есть взвешенная «энергия» управления; он включается в критерии для того, чтобы ограничить управление. Требуемое ограничение на управление, которое в явной форме не учтено в постановке задачи (10.120), (10.121), может быть обеспечено соответствующим выбором весовой функции R (t). Матрицы Q (/) и R (t) в общем случае выбирают зависящими от времени. Такой выбор, в частности, связан с тем, что начальные отклонения от свойства систем не зависят: они определяются начальными условиями. Поэтому их следует выбрать такими, чтобы начальные ошибки меньше влияли на величину критерия, чем такие же ошибки, возникающие в последующие -моменты времени. На основе приведенных соображений нельзя выработать рекомендации, которые позволили бы однозначно определить матрицы, входящие в критерии оптимальности. Один из возможных способов выбора этих матриц предложили А. Брайсон и Хо Ю-ши [51. Они рекомендуют брать их диагональными со следующими элементами: обратные элементы 1/Дг матрицы F равными максимально допустимым значениям [л:- (tf)], обратные элементы l/qu матрицы Q - произве- [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [ 108 ] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |