
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [ 119 ] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 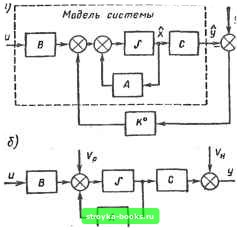 Рис. 10.7 Несингулярная задача оценивания (10.189)-(10.191) при некоррелирова н ных шумах впервые была решена Р. Калманом и Р. Бьюси. Ее решение, представляющее собой оптимальный наблюдатель, называется наблюдателем (рцениттелем) или чаще фильтром Калмана-Бьюси. Заметим, что Р. Калман и Р. Бьюси рассмотрели случай. когда U = 0. Сравнивая уравнения объекта (10.189) и оптимального наблюдателя (10.192), замечаем, что их правые части отличаются только последними слагаемыми: в уравнении наблюдателя вместо шума объекта появляется слагаемое, пропорциональное разности у - Сх. Эта разность между измеренным текущим значением выходной переменной и его оценкой у = Сх называется невязкой. Структурная схема наблюдателя Калмана-Бьюси рис. 10.7, а) включает в себя как составную часть модель исходной системы (рис. 10.7, б). Ее отличие от заданной системы состоит только в том, что она имеет дополнительно обратную связь по невязке. Интересно отметить, что наблюдатель Калмана-Бьюси имеет такую же структуру, что и наблюдатель полного порядка в детерминированном случае (см. рис. 10.3). Соотношения (10.192)-(10.195) определяют также решение задачи линейного оптимального оценивания, которая отличается от задачи оптимального оценивания (10.189)- (10.191) тем, что: а) о законах распределения шумов и начального состояния никаких предположений не делается (не требуется, чтобы они были гауссовскими); б) нужно найти линейный оптимальный наблюдатель, т. е. оптимальный наблюдатель в классе линейных систем. Другими словами, если шумы и V„ и начальное состояние х" не являются гауссовскими, то наблюдатель Калмана - Бьюси является оптимальным. вообще говоря, только среди линейных наблюдателей (систем). Покажем, что наблюдатель Калмана-Бьюси является линейным оптимальным наблюдателем. Достаточно доказать, что оценка, определяемая наблюдателем Калмана-Бьюси, минимизирует функционал У ==.М{аГх(0-а(0} (10.196) при произвольном «-векторе а. Действительно, если оценка X (/) минимизирует функционал (10.196) при произвольном а, то она," очевидно, минимизирует функционалы 7,-=М {Xiit) -Я(ОГ. «•= 1,2, ... , п, которые получаются из (10.196) при соответствующем выборе вектора а, и соответственно сумму 2 i=M{ [xAt)-i(t)]% представляющую средний квадрат ошибки оценивания (10.191). Сначала примем и = 0. Воспользуемся схемой доказательства, основанной на преобразовании задачи линейного оптимального оценивания к задаче оптимального управления [161. Так как отыскивается линейный оптимальный наблюдатель, то линейная комбинация ах (/J, как и сама оценка х (у, представляет собой линейный функционал от функции у (т), /о 1. которая является входным воздействием искомого н аблюдател я: axifi) = j и-г{х)у{х)с1х+Ых». (10.197) Найдем весовую функцию и (т) и постоянный вектор Ь, при которых оценка х (t), определяемая последним соотношением,, является несмещенной и оптимальной в смысле минимума критерия (10.196). Подставим в (10.197) выражение для у (т) из (10.190): ах (/,)= J К(т)С(т)х(т) -f йЧт)Х XV„(T)ldT-fbrxO. (10.198) Введем векторную переменную х, определяемую уравнением х = -Ах + Си, to < / </i. (10.199) при граничном условии x(/i)=-a. (10.200) Очевидно, ax(/i) = x(o)x(g+J £?[хГ(т)х(т)1. Так как в силу уравнений (10.188) и (10.199) (напомним, что рассматривается случай и (t) ~ 0) d [х х] =х xdT Н-х X dT = (й Сх + х V) dx, &т X {tl) = х"; (о) X {to) + J (и Сх + х Vo) dx. Вычитая из этого соотношения (10.198), получим X {tl) -а X {tl)=х"" {to) X (/«) -? + + ((Fv„-uV„)dT, откуда , , М [а X (tl)- 1 (tl)] = I х"" (4) - х". . Из последнего равенства следует, что при х(/о) = Ь (10.201) оценка а х (ti) линейной комбинации а х (ti), определяемая соотношением (10.197), будет несмещенной при всех а и и (t). Из него также следует, что 7 - М [а X (tl) - а X (ti)] = М [ х"" (to) х (to) -. -bх"] + ]]м\[х(т) Vo(т)- (т) V„(т)] X X [хЧт) Vo (т) - й(т) V„(T)]n dx dx. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [ 119 ] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |