
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [ 12 ] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] среди этих уравнений могут быть уравнения, имеющие устойчивые и неустойчивые решения с различными переходными процессами. Любое из них пригодно для нахождения автоколебаний, но, если не дано специального обоснования для каждого конкретного случая, в общем не позволяет исследовать устойчивость и неустановившиеся режимы. Поэтому эквивалентная линеаризация по рассмотренному выше способу для нелинейных элементов с неоднозначными характеристиками может быть использована только для нахождения параметров первых гармоник автоколебаний, исследования же переходных процессов, иногда рекомендуемые в литературе, с помощью описания нелинейного элемента уравнением (7.37) в общем случае необоснованны. § 7.7. Метод гармонического баланса Метод гармонического баланса не использует гипотезы порождающей системы, а основан на следующих рассуждениях. Разомкнем систему перед входом нелинейного элемента. В автоколебательном режиме первые гармоники величин х к у на входе и выходе нелинейного элемента соответственно равны: X = Asin Qt; у = А (g sin Qt + b cos Qt). (7.40) Эти уравнения более удобно записать в комплексной форме: х Ле>"; yA{gjb)ef° = {g + jb)x. На выходе разомкнутой системы имеем . - , •. z=W(jQ)(g+jb)xWU)W„,,(A)x. Автоколебания в замкнутой системе будут существовать, если выход и вход разомкнутой системы связаны соотношени-ями Z = - х, которые имеют место и в замкнутой системе (рис. 7.34), или . [l + W(jii)W„M]x = 0. l.is.-, Так как равенство справедливо для I-1 w... LJ любых t, приравняем нулю выражение в квадратных скобках: V/Qa Рис. 7.35 (7.42) Из (7.41) легко получить равенства W (/£2)=-1 / Г(Л) = -1 /(g + ib) = G„., (И); :: G ijQ) =-W„., (Л) = - (g + /Ь). Первое из этих равенств было впервые предложено Л. С. Гольдфарбом (СССР), второе, независимо, но несколько позднее, - Р. Кбченбургером (США). Равенства используются для графоаналитического решения задачи. " По методу Гольдфарба строят (рис. 7.35, а): W (JQ) амплитудно-фазовую характеристику линейной части системы; - С„.з (А) = - I/ (g + ib) = - \/W„.s - кривую гармонического коэффициента передачи, или, по американской терминологии, описывающей функции. На первой точками отмечают ряд значений й, й,..., на второй - значения Л, А, - • В точках пересечения кривых с помощью интерполяции между соседними с ними значениями fij, iii+i и Aj, Aj+i находят значения частоты и амплитуды Лд автоколебаний. Пь Методу Коченбургера эти параметры сходным образом находят по точкам пересечения кривых G {}Щ и - 1F„ а (Л)= = -{g + ib) (рис. 7.35, б). Пример 7.1. Линейная часть системы состоит из двигателя постоянного тока и безынерционного усилителя. Ее передаточная функция где 7\ - электромеханическая постоянная времени; - электромагнитная постоянная времени;-общий коэффициент усиления .линейной части 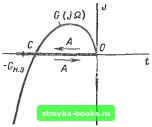 Нелинейный элемент - поляризованное реле с зоной нечувствительности. Реле срабатывает мгновенно. Его статические характеристики f м = /(л)=- 0; X > а; - а< X < а; - М; х<-с1, где /М = const. Вычислить обратную аыплитудно-Рис. 7.36 фазовую характеристику линейной части. Подставляя в выражение обратной передаточной функции s = jQ н разделяя вещественную н мнимую части, получим С (/Q) = (I () [/fi (I - Г, Гг)- Q2 Til. Годограф С (/Q) (рнс. 7.36) пересекает действительную ось, когда его мнимая часть обращается в нуль, т. е. при 1 - QITT = 0. Частота Qg, обращающая в нуль это выражение, является одновременно порождающей частотой, т. е. частотой автоколебаний Qo = УЩ\т7Г. • • • Отрезок с действительной оси от начала координат до точки перс-сечения равен с = Q-T/K = 1/(К72)-Из (7.34) определим {/„ ~ 0; 6 = 0; g==[4M/{nA)] f sinijjdrf = [4Ж/(.пУ1)] cosa, о где а находят нз соотношения х = А sin а = а, нлн cos а = = Vl - аЧА-. Окончательно g.(). J[4A/(")l Vi-a/A. Ла; [О, А <. а. Амплитуду колебаний найдем нз уравнения g{A).=.im/(nA)] l/l-aV=c=l/(/Cr2). В данном случае решение можно получить аналитически: Л = (2 1/2 КТгМ/п) Vl ±Vl - naymTl M). Точка пересечения одна, но ей соответствуют два значения амплитуд. Первое (меньшее) получается при движении вдоль оси в направлении возрастания А при движении вправо, при дальнейшем возрастании амплитуды направление движения в некоторой точке изменится. Второе пересечение получится при большей амплитуде прн движении влево. Если IKTM < или а > 2КТМ1п, то пересечения характеристик не произойдет и автоколебания ге возникнут. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [ 12 ] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |