
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [ 136 ] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] постоянных или нулевых значениях остальных координат отыскивают минимум dJ {x)/dxi. После обращения в нуль dJ {х)1дх = О найденное значение Ху закрепляется и изменяется координата х до обращения в нуль частной производной dJ (х)/(Эх2 = 0. Таким образом находят частные экстремумы по всем п координатам. Затем осуществляют повторный цикл изменений начиная с координаты xj,- и так до тех пор, пока найденная точка экстремума не окажется экстремальной для всех координат. Таким образом, регулярность метода определяется очередностью изменения координат, однако к недостатку данного метода следует отнести произвольность в выборе нумерации координат, что может в отдельных случаях существенно удлинять поиск. Метод градиента. Градиентом выпуклой дифференцируемой функции J (Xi, Xg, ...) называют вектор, проекции которого на оси координат Xi, Xj, ... соответственно равны частным производным дЛдХу, dJ/dxs..... Каждая из составляющих градиента может быть приближенно определена по двум замерам значений функции J (у) в близких точках х -f- А. т. е. grad J (х) [J (X + А) - J [х - Л)1/(2Л). В том случае, если функция J (х) зависит от нескольких переменных, т. е. J (Xj, Xj.....х„), градиент определяют по всем переменным: {l/Ai){y(Xi + Ai), х.,...,х„1-У 1х,.х2.....х,Л}; (I/A2) {J (х, (Xj Ч- Ао)..... xJ - У [X,, Хг.....X,,}; (1/А„){Ух„ х.г,...,(х„ -f А,,)] -y[Xi,x.,..... х„\}. (П.20) После определения направления градиента осуществляют переход в новое положение по каждой координате в зависимости от максимальной величины и направления градиента. В методе градиента используют свойство уменьшения величины градиента по мере приближения к экстремуму. Это легко проследить на рис. 11.6, наблюдая за изменением наклона касательных к кривой J (х). 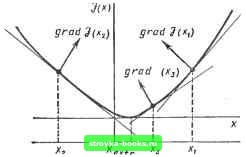 Рнс. 1 1.6 Координаты каждого последующего положения определяют таким образом: х(2)=х()-1-с(]/Д,) 4"..... 4"]- -/(х<>, х.<",..., x,V>]}; х<> " + о (1 /Дг) {J[x[\ (xi 4- До),..., ] - -У[л-),х(),.... , ("-21) х!,>=-х;,"-Ьа(1/А„){Ух<",х<)....,(4"4А„)--У1х<), х<>,...,х<,"И. Следовательно, в методе градиента процесс поиска разделяется иа два этапа. Вначале делают пробный шаг лля определения величины и направления градиента в соответствии с алгоритмом X,- = Хо + Д,-. i = 1. 2, .... п. (11.22) где Хр - координата вектора начального состояния; х,- - координата вектора пробного состояния; g - величина пробного шага; Д,- - единичный вектор отклонения по заданной координате. Затем осуществляют одновременное рабочее смещение в направлении градиента всех координат в соответствии с уравнением X =- х„ ± а grad J (х). (11.23) 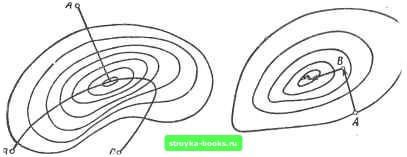 Рис. 11.7 Рис. 11.8 где X - вектор нового рабочего состояния; а - величина рабочего шага. Иногда для ускорения поиска пробные и рабочие шаги совмещают, т. е. каждый рабочий шаг становится пробным шагом для последующего состояния. На рис. 11.7 показаны траектории движения из начальных точек А, В, С к экстремуму по направлению градиента. Кривые движения нормальны к линиям постоянных значений функции качества J (х). Нетрудно видеть, что при наличии у функции качества так называемых «оврагов» или «гребней» движение по градиенту может стать очень извилистым, кроме того, направление градиента зависит от выбранных масштабов изменения координат по каждой оси, т. е. при неблагоприятных масштабах по осям поиск может значительно затянуться. Метод наискорейшего спуска. Метод наискорейшего спуска является модификацией метода градиентного поиска. Здесь также определяют градиент в исходной точке, но затем движение происходит по выбранному направлению (Л, В, ...) до тех пор, пока функция качества продолжает уменьшаться (рис. II.8). Затем вновь определяется направление градиента и организуется прямолинейное движение в этом направлении до уменьшения функции качества и получения минимального значения ее по данному направлению. Метод наискорейшего спуска значительно сокращает процедуру поиска экстремума по сравнению с методом градиента, поскольку в нем уменьшается количество точек, в которых осуществляется определение величины и направления градиента. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [ 136 ] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0012 |