
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [ 145 ] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] пульсной переходной функции k (f). Имеется ряд способов измерения \. При непосредственном измерении по уравнению (ПЛИ) без правой части y/dt + cog у)/2соо dy/dt (11.116) возникает необходимость в получении информации о второй производной dy/dt. Если возможность получения информации о второй производной отсутствует, то можно воспользоваться способом амплитудного сравнения, т. е. Л,= се-"«/(2 VT. (11.117) Л, + 2== ce-( + )"S/(2 КГО. (11.118) Тогда разность значений амплитуд зависит от исходного коэффициента и текущего коэффициента Ij, т. е. Д.4, се ••W(2rT)(l ge-«5/yr:T). (11.119) В линейных системах частотные передаточные функции также достаточно полно характеризуют динамические свойства системы управления, поэтому идентификация и последующая стабилизация амплитудной и фазочастотной характеристик могут служить эффективным способом адаптации свойств самонастраивающейся системы в процессе ее функционирования. Общий принцип определения одного или нескольких значений частотных характеристик заключается в подаче на вход системы гармонического сигнала заданной частоты и амплитуды: Xi = Ai sin coif, i 1, 2, п. (11.120) Выходной сигнал пропускают через фильтры, настроенные на заданную частоту. В результате можно получить значения амплитудной В («/) и фазовой ф (oj) частотных характеристик, а также вещественной Р (ы;) и мнимой Q (cOj) характеристик: W (/С),) = Р Ы -hQ (Щ) i - В (со,) е"" . (11.121) Амплитудно-частотная характеристика В (ш;) получается простым сравнением амплитуд входных гармоник и гармоник на выходе фильтра. Труднее определять фазочастотную характеристику. Один из способов определения заключается в подаче гармонических сигналов Xi = /IfSin mt (на систему) и xt = = Ai cos (i)it (на эталонный фильтр). Выходные сигналы системы tji и эталонного фильтра yi после перемножения дают Уг Уо1 Ai В («г) sin (со, t + ц>) А В, (ы,) cos (оц t + ф.,.) = = 0,5Л?В(ю4) В, (c-j;) fsin (фг-Фэ,•)-sin(2c-J,•.-ф,-фg,.)]. (11.122) Разность фаз системы и эталонного фильтра на частоте со, определяют по постоянной составляющей (11.122). Если на систему и эталонный фильтр подается один и тот же сигнал Х; = Л; sin со,-/, то выходные сигналы системы и фильтра вычитаются: Уо.- -Уь = Bg (CO;) sin (Wj t + Фэ,-) -Л; В (ю,) sin (со,. / -f ф,) = = Ai В (со,) sin (со,. ?-Ьдф;), (11.123) где Дф; = arctg (j) Ф-5 (j) i" ft . В (to,-) cos fpaj- в (to,.) cos ф; При В (coj) == Вэ («,) разность фаз Лфг = 2 arcsin [ДВ {1,ц)/2В (oj;)!- (11.124) Вещественную и мнимую частотные характеристики можно определять, перемножая выходной сигнал системы Л,-В (со;) X X sin {wit + ф;) соответственно на sin со,- и cos со,-/ и интегрируя эти выражения Eia интервале Т -= 2я/г/со,-, где п - целое число, т. е. Р (c-j,) =[2В ((0;)/Г1 cos ф,- sin ю,- t di = В (со,) cos ф,.; Q (со,.) =l2B (со,.)/Г1 sin ф,- j" cos ю; / Л = В (м,) sin ф;. (11.125) Примеры беспоисковых самонастраивающихся систем Самонастраивающаяся система измерения скорости движения с коррелятором. Систему используют для измерения скорсх:ти движения листового металла при прокатке. Блок-схема системы приведена на рис. 11.16. От двух источников 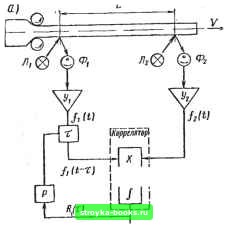 ~Г \J,(t-r)fi(t]  Рис. 11.16 света Лг и Лг (рис. И. 16, а) на движущийся металл проецируются световые пятна, которые, отражаясь от неровностей поверхности металла, попадают на фотоэлементы и Ф. После усиления сигналы ijt) и (i) поступают в коррелятор, причем сигнал (i) пропускают предварительно через устройство переменной задержки времени т. Задержка т регулируется до значения тт, равного времени перемещения полосы металла на расстояние L между двумя источниками с постоянной скоростью V, т. . е. Тг L/V. (11.126) Именно для такого момента задержки почти полностью совпадают искусственно задержанная функция (t - т) и функция /г (0> как естественно отстающая функция fi (t) (рис. 11.16, б), т. е. h it-iT) « h if). (11.127) [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [ 145 ] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0014 |
|||||||||||