
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [ 147 ] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] WoiiP) Цоа (Р) Уо, (Р) (р) «=1, 2.....п. Настройка параметров Xi, Xj,.... х„ производится в соответствии с уравнениями .dXi/df=---XidEVdXi=liEW„i ip,x) Км; (11.143) dxJdt XiEUi. (11.144) § 11.4. Системы с адаптацией в особых фазовых состояниях Рассмотренные в предыдущем параграфе адаптивные системы с контурами самонастройки обладают весьма существенным недостатком, вызванным наличием в них сложно реализуемых вычислительных блоков для поискового или аналитического определения условий экстремума заданного функционала качества. Часто реализация контура самонастройки приводит к усложнению конструкции системы управления и к снижению надежности ее функционирования. В отдельных случаях удается решить задачу адаптации более простыми средствами, используя, например, особенности нелинейных систем. В нелинейных системах могут возникать при определенных условиях особые режимы - автоколебательные или скользящие. Иногда такие режимы бывают вредными или недопустимыми с точки зрения функционирования объекта управления, тогда приходится принимать специальные меры для ослабления действия этих режимов. Однако в адаптивных системах факт возникновения особого режима может быть использован для получения дополнительной информации об управляемом процессе либо особый режим преднамеренно организуется в системе, придавая ей новые свойства, в частности свойство адаптации к параметрическим или внешним возмущениям. , Рассмотрим два класса систем с адаптацией за счет особых : режимов: релейные автоколебательные системы и адаптивные "системы с переменной структурой. Релейные автоколебательные системы управления. В нелинейной системе, состоящей из релейного элемента и линейной части с передаточной функцией Wo{p) (рис. 11.19), используя метод гармонической линеаризации, можно определить зависимость параметров автоколебаний от параметров линейной части. Предположим, что передаточная функция линейной части Wo iP) = ko тр (1 + Т) (1 + Т,р)]. (11.145) где Ti, - const; ko (t) - переменный коэффициент усиления. Уравнение релейного элемента F (х) = Uo sign X. (11.146) При g (t) = О можно записать общее уравнение для оператора нелинейной системы: Ti П + (71 + Т2)р + Р + К (О По sing х = 0. (11.147) Гармоническая линеаризация релейного элемента дает следующую зависимость: F (х) = 4ко/(яа). (11.148) Поэтому (11.147) можно записать так: Ti Т, р + (Ti + Гг) р + рЛ-К т 4н.о/(зта) =0. (11.149) Находя периодическое решение уравнения (11.149) при условии р = /О), находим амплитуду и частоту автоколебаний: а = l4feo if) Uoln] [Ti Гг/(Г1 + Т,)]; со = I iVT\T\ (I I -150) Отсюда видно, что при параметрическом возмущении в виде изменения коэффициента усиления объекта ко [f) амплитуда автоколебаний также будет изменяться. Поддерживая амплитуду автоколебаний на заданном первоначальном уровне, можно создать систему, адаптирующуюся к указанному параметрическому возмущению. Таким образом, параметры особого режима в нелинейной системе могут быть использованы в y(t) 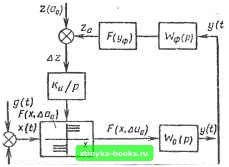 Рис. 11.20 качестве дополнительной рабочей информации для обеспечения стабильной работы системы вблизи экстремального режима. На рис. 11.20 приведена структурная схема адаптивной автоколебательной системы с регулируемым уровнем ограничения релейного элемента. На основании (11.150) амплитуда автоколебаний может поддерживаться на постоянном уровне при изменениях (t) за счет изменения уровня ограничения реле Iuq + Аи (f)]. Уравнения системы записываются следующим образом: уравнение релейного элемента F 1х, Амо (t)] = [«о + Д"о (01 sign X (0; (11.151) уравнение фильтра, настроенного на частоту автоколебаний Gq, y<i. = kpy(t); (11.152) уравнение двухполупериодного выпрямителя сигнала автоколебаний 2, = £/ф; (11.153) уравнение исполнительного устройства для перестройки уровня ограничения релейного элемента Ащ (t) = (kjp) Az, (11.154) где Az =i z (oo) - Za; уравнение основного контура Tl n+ (Tl + p+p + ko (0 l«o + Д«0 (Olsign X it) = 0. (11.155) После гармонической линеаризации (11.155) получим ТгТр+{Ti + Tfp + p + ko (0 4 [«о + Аыо (t)]/na = 0, (11.156) [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [ 147 ] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |