
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [ 149 ] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 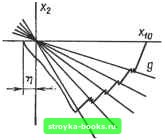 5 = Wy2=0 Рис. 11.22 (11.166) при минимальных значениях ui {f) из диапазона max- На поверхности go (в данном случае прямая) возникает скользящий режим при любых значениях а,- (/) из заданного диапазона. Факт возникновения скользящего режима регистрируется индикатором скользящего режима, выходной сигнал которого скачкообразно изменяется при уменьшении относительной длительности пребывания системы в состоянии одной из имеющихся структур, т. е. при повторных изменениях знака функции go- По сигналу индикатора скользящего режима функция переключения перестраивается с go на gi l = (Cmin + Ac)Xi + X2. (11.168) В системе вновь возникает скользящий режим, но уже на линии переключения = 0. С помощью индикатора скользящего режима происходит дальнейшее перестроение функции переключения gi = (Cmin-1-/Ас) Xl + Хг (11.169) до тех пор, пока значение коэффициента {с1-\-1Лс) не превысит значение сах. после чего скользящий режим по условию (11.166) возникнуть не сможет и перестроение функции переключения закончится. Движение фазовой точки после того момента будет происходить по близкой к границе gn)ax=Cmax Xi-\- + Хг = о фазовой траектории одной из структур без скользящего режима (рис. 11.22). На этом же рисунке видно, что шаг приращения Ас должен выбираться в зависимости от допустимого значения перерегулирования т) в переходном процессе. Таким образом, за счет поиска предельного по условию (11.166) режима работы поддерживается максимальное быстродействие системы управления при изменениях параметров объекта. Адаптивная система с переменной структурой, использующая информацию о внутренних координатах, На основании p -I Рис. 11.23 (11.165) поверхность скольжения g==0 формируется из n фазовых координат системы л;,, i = 1, 2, п. Поэтому при создании системы с переменной структурой требуется информация о производных сигнала ошибки х. Количество производных определяется порядком исходного дифференциального уравнения. Хорошо известно, что получение точных значений производных высокого порядка путем многократного дифференцирования сигнала х является сложной технической задачей. На практике при высокой размерности исходных уравнений приходится заменять часть недоступных точному измерению фазовых координат xi различными внутренними координатами системы, связанными с фазовыми координатами через параметры объекта управления или регулятора. При этом удается получить преимущестю в точности воспроизведения значений координат и снизить влияние помех на систему. Однако в системах с переменной структурой указанная замена часто оказывается неэквивалентной. На рис. 11.23 представлена система с переменной структурой. В управляющем устройстве УУ формируется закон управления i= 1 а,прих,>0, il. I Pi при Xig<cO, a,npHx.g>0,. Р2прих2<0, (11.170) жения; A, А, Ui, p, a, fij - постоянные величины; «1 = = - Pi, аг = -Pa; Cj, -постоянные коэффициенты. Для формирования закона управления (11.170) необходимо продифференцировать сигнал ошибки х два раза и получить фазовые координаты х и х., где Xj = dxildt, Xg = dxjdt. После двукратного дис}х)ерениирования сигнала ошибки с помощью реальных дифференциаторов уровень помех на выходе второго дифференциатора может возрасти до недопустимых значений. В этом случае может оказаться более выгодным использовать вместо координаты Хз внутреннюю координату 2з, доступную для точного измерения непосредственно с объекта управления. Тогда поверхность скольжения будет иметь следующий вид: = c,xi4-+ 3 = 0. (11.171) Внутренняя координата 23 связана с координатой ошибки Xj соотношением 2з = [1/2 (03 (01 Р И + T(t)p]Xi. (11.172) Подставив (11.172) в (11.171), получим g (t) = CiXi + СгХг + [l/k (t) k, (01 p [i + Гз (0 p] Xl = = (0 .4 + Cs, (t) Хз + X3 = 0, (11.173) где Cl (t) - cife (0 3 {t)/T, it); {t) = l(ck, {t)k,{t)/T,(t) + 11. Таким образом, после замены Xg на 23 положение поверхности скольжения в фазовом пространстве определяется в зависимости от перемегшых параметров объекта управления ki (0. 13 (0> 3 (О- Следовательно, дпижение в скользящем режиме, происходящее по указанной поверхности, теперь уже не будет независимым от параметрических возмущений, поскольку сама поверхность скольжения при изменениях указанных параметров будет подвижна. Это приведет к тому, что качество переходных процессов в системе будет существенно изменяться прн параметрических воздействиях. Например, при значительных диапазонах изменения параметров 2 (0. з (0. Тз (О длительность переходных процессов может изменяться в несколько раз. Если показатели качества должны поддерживаться в жестких пределах независимо от изменяющихся пара-. метров, тогда произвольные смещения поверхности скольжения должны устраняться, т. е. поверхность скольжения долж- [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [ 149 ] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |