
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [ 150 ] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] на в процессе изменении возвращаться в исходное состояние. Однако такой способ адаптации требует дополнительной информации об изменяющихся параметрах объекта управления. Обычно возможности для получения такой информации ограничены. Поэтому возможен другой способ адаптации характеристик системы в условиях действия параметрических возмущений, который базируется на использовании не только разрывных коэффициентов в функции управления и, но и разрывных поверхностей скольжения g. В фазовом пространстве системы (рис. П.24) формируются две поверхности скольжения, так же как и в случае (11.173), т. е. с помощью внутренней координаты Zg: gi (О == (t) + cl (О X, + Хз = О, (11.174) g, (О == с» (О xi + (О + Хз = 0. Причем коэффициенты с"* (О и Сг" (/) подбирают, исходя из заданных требований к качеству переходных процессов, но так, чтобы во всем диапазоне изменения параметров объекта траектории движения в скользящем режиме по поверхности были только апериодические, что соответствует сильно демпфированному движению. Коэффициенты с? (/) и (О поверхности = О, наоборот, подбирают из условия слабо демпфированных движений по траекториям скольжения на gi = 0. Адаптивный закон управления позволяет объединить обе поверхности скольжения в оДну, но разрывную поверхность скольжения, что эквивалентно скачкообразному изменению положения поверхности скольжения в фазовом пространстве. и = tpiXi -f 1152X2 «1 при Xi g (Г) > О, (11.175) Pl при Xigr(f)<0, «2 при X2g(0>0, р2 при Хг g (t) < О, 11 К Л; 1112<Лг; gf)\gi (О при Xi (Dxi -{- Хг) > О, 1 g2 (О при Xi (Dxi + Xi) < 0; gi (О - (t) xi H- c»» (t) Хг + Хз = % + с" 2 + гз = 0; g2 (О = (О Хг + (О 4- Хг - Хх -f х + = 0. 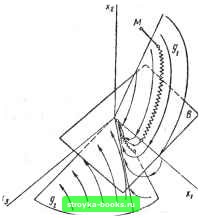 Рнс. 11.24 Все коэффициенты а,, а, Pi. Рг. сЧ\ с1\ с\\ с1\ D являются постоянными величинами. Только коэсрфициен-ты cV{t), cV{t), cVit), cV {t) - переменные в силу связи внутренней координаты гз и Хз. D выбирают из условий перехода изображающей точки с gi{t) на g«{t). Разрыв поверхности скольжения g (f) производится в месте пересечения gi {t) с плоскостью В = Dxi + Xj = 0. Все постоянные коэффициенты (в частности, коэффициент D) выбирают как из условия попадания изображающей точки из любых начальных гюложений на обе поверхности скольжения, так и из условий обеспечения скользящих режимов на каждой поверхности скольжения gi(f) и git) при всех изменениях параметров объекта внутри заданного диапазона. На рис. 11.24 показана фазовая траектория, начинающаяся в точке М. Изображающая точка, попав на поверхность скольжения gi. далее перемещается по этой поверхности в скользящем режиме вплоть до плоскости В. В этот момент происходит разрыв и перемещение поверхности скольжения [изменение (t) на g (t)\. В результате этого скользящий режим прекращается изображающая точка в силу уравнений одной из структур движется в направлении измененной поверхности скольжения, попадает на эту поверхность и заканчивает движение в скользящем режиме уже по поверхности gj. Эффект адаптации зесь проявляется за счет того, что, хотя обе поверхности скольжения gj (t) и g {t) в результате параметрических возмущений смещаются в фазовом пространстве, это практически не сказывается на показателях качества переходных процессов, поскольку заключительный этап движения всегда происходит по сильно демпфированной траектории скольжения на поверхности g (t). При очень больших диапазонах изменения параметров объекта разрыв поверхности скольжения g (t) на пересечении с неподвижной плоскостью В = Dx, + = О оказывается эф())ективиым только для части диапазона изменения парамет- pon. Этот недостаток устраняется за счет формирования подвижной плоскости В (t), обеспечивающей разрыв и переключение g (t). Такой эффект получается при введении в уравнение плоскости разрыва В внутренней координаты вместо фазовой координаты х. Плоскость В, перемещаясь вверх или вниз однозначно с изменениями параметров объекта, вносит соответствующее Опережение или запаздывание по моменту разрыва плоскости скольжения g (t), тем самым улучшаются условия для попадания изображающей точки после разрыва с поверхности скольжения gi на поверхность g- Закон управления в этом случае приобретает следующий вид; g{t) = и = ipi Xi + ijja х; fa, при Xigr(0>0, г1),Л1. i Pi при Xig(0<0, г1згК Лг; аг при Хг g {t) > О, , р2 при Хг g (П < 0; gi (t) при Xi (Dl Xi -Ь Fy Zj) > 0, gi (t) при Xi (Dl Xi 4 f 1 Zs) < 0- (11.176) Bee коэффициенты являются постоянными величинами, а 1 (О и gi (О такие же, как и в (11.175). К преимуществу адаптивных систем с переменной структурой указанных типов слеиует отнести высокую эффективность адаптации при простом конструктивном исполнении системы. Выбор постоянных настроек регулятора н логическая коррекция структуры в зависимости только от фазового состояния системы управления существенно упрощают ее синтез. § 11.5. Обучающиеся системы Обучающиеся системы являются наиболее сложным и пока мало изученным классом адаптивных систем. Такие системы создаются на основе принципа обучения, заключающегося в постепенном накоплении опыта формирования поведения системы при высокой степени неопределенности ее исходных состояний, по результатам которого происходит улучшение функционирования системы. Характер накопления опыта при [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [ 150 ] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0014 |