обучении весьма миогообразен, например опыт может быть накоплен положительный или отрицательный, систематизированный или случайный, собственный или привнесенный извне, имитационный (искусственный) или естественный и т. д. Однако у всех способов накопления опыта есть достаточно общая черта - постепенное выделение «области знаний» из всей совокупности «незнания». Поэтому в теории обучающихся систем эта особенность нашла отражение в достаточно быстро развивающемся направлении, связанном с созданием автоматических систем классификации или распознаванием образов. Под классификацией или распознаванием образов здесь понимается установление по результатам накопленного опыта границ между определенными классами сложных ситуаций. Задачи распознавания и классификации встречаются часто не только в технических приложениях, но и в таких областях, как медицинская диагностика, геологическая разведка месторождений, прогнозирование погоды и т. д.

Задача автоматического обучения классификации формулируется следующим образом. Каждой возможной ситуации из множества рассматр-гваемых ставится в соответствие точка некоторого пространства х. Заранее известно, что в пространстве X необходимо выделить две нли большее число областей или классов ситуаций. Расположение границ между областями неизвестно и нет определенных правил, по которым можно определить принадлежность той или иной точки любой из заданных областей. Цель обучения заключается в гюстрое-нии поверхности, разделяющей предъявляемые точки из указанного множества на заданное число классов. Принципиально существует два подхода к обучению такому разделению. В первом случае, при обучении с поощрением, классифицирующему автомату предъявляют ряд случайных точек из множества в пространстве х и сообщают информацию о принадлежности этих точек определенным классам. После определенного цикла обучения на таких примерах автомат строит разделяющую поверхность и может в дальнейшем отличать принадлежность разным классам не только предъявленных ему точек-примеров, но и любых других точек в пространстве х.

В случае обучения без поощрения информация о принадлежности точек разделяемым классам отсутствует. Здесь автомат по наблюдению предъявляемых точек определяет факт компактного расположения нескольких из них и затем строит разделяющие поверхности на основе выбранной меры бли зости компактных групп точек к разделяющей поверхности

Объективная сложность обучения как с поощрением, так и без поощрения заключается в том, что не всегда классы из близко расположенных друг к другу точек строго отделимы, т. е. возможны пересечения классов, когда одни и те же точки принадлежат разным классам.

На рис. 11.25 показаны различные классы множества точек (отмеченные в одном случае X и в другом 0). В первом случае (рис. 11.25, а) классы просто могут быть разделены прямой линией (показана пунктиром); в другом случае (рис. 11.25, б) классы можно разделить достаточно сложной кривой; в третьем случае (рис. 11.25, б) невозможно разделение классов какой-либо одной прямой или кривой линией.

Для хорошо разделимых классов используют достаточно простые алгоритмы автоматической классификации, основанные на аппроксимации разделяющих поверхностей отдельными участками гиперплоскостей. Для менее разделимых классов приходится использовать вероятностные методы, основанные на определении, вероятностных характеристик принадлежности то.чек пересекающимся классам.

Метод секущих плоскостей. Пусть требуется разделить три фигуры, состоящие из набора точек. В автомат вначале вводят значения двух точек 1 и 2 (рис. 11.26, а). Автомат запоминает их и строит произвольную плоскость, разделяющую эти точки, причем точка 2, лежащая выше плоскости /. относится к классу В. После предъявления точки 5.эта точка оказывается выше плоскости / и, следовательно, должна быть отнесена к классу В, однако известно, что эта точка из класса А. Это противоречие между точками 2 н 3 разрешается построением новой плоскости . При появлении следующих точек 4 и 5 противоречий не возникает и автомат не проводит новых плоскостей. При появлении точки 6 (рис. 11.26, б) возникает противоречие между этой точкой, принадлежащей

о * о о е о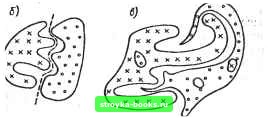

о о

S) я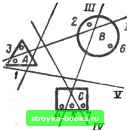

Рис. п.26

классу В, и точками 4 и 5. Тогда сначала строят плоскость /, разделяющую точки / и 6, а затем плоскость IV, разделяющую точки 5 и 6. Постепенно области, где точки противоречат разделению, сужаются и вероятность возникновения противоречий уменьшается. После определенного цикла обучения построению разделяющих поверхностей можно и запомненных поверхностей отбросить лишние участки и получить разделяющую поверхность, состоящую и нескольких гиперплоскостей. В дальнейшем обучение заканчивается и все последующие точки будут отнесены к соответствующим фигурам или близким к ним областям.

Метод потенциальных функций. Обычно без нарушения общности задача обучения классификации рассматривается как задача разделения на два класса: Q к R. В детерминированной постановке оба класса не пересекаются друг с другом и могут быть четко отделены один от другого.

Метод потенциальных функций позволяет за конечное число показов входных сигналов из обучающей последовательности построить разделяющую функцию Ф(л:), принимающую положительные значения в точках, соответствующих классу <3, и отрицательные значения в точках, соответствующих классу R. При построении в режиме обучения с поощрением используется информация о знаке разделяющей функции, т. е. восстанавливается функция Ф(л:) по нерегулярно появляющимся отдельным ее точкам. После построения разделяющей функции, т. е. по окончании процесса обучения, любая входная ситуация, принадлежащая классам Q или R и появляющаяся на входе автомата, правильно опознается автоматом.