
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [ 155 ] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] Далее, минимизируя средний риск (11.223), можно получить разделяющие функции /ь. Например, для случая двух максимумов М = 2 (или классов) средний риск = J f 1 (х, с) р (X) dx + j f 2 (х, с) р (х) dx. (11.227) Условия минимума R: min {вг (X, с) Vc f 1 (X, с) + вг (х, Г) Vf 2 (х, с)} = 0, (11.228) „ , f 1 при xXi, „ . (О при X € Xi; гдев1(х,с)== в2(х,с)= (О при Xg Лг; 11 при Xg Лг. Разделяющая функция / 12 имеет вид fi2 (X, с) = Fl (х, с) - Fa (X, ?) =- О. Отсюда дискретные алгоритмы самообучения c[n] = c[rt-1]-ri[nJVcFi(x[tt], 7ln - l]), (11.229) если /i2(x[n],?[tt -1])= Fi(x[tt], c[tt -1]) - -F2(x[rt],7[rtl]X0,. c[tt] = c[tt -1]-r2[tt]VcF2(x[tt], c[n-1]), (11.230) если /i2(x [n], с [tt- 1]) > 0, где Tl и Га - матрицы коэффициентов, определяющие сходимость вектора с к оптимуму. Персептронная модель автоматической классификации Впервые принципы автоматической классификации были реализованы американским ученым Ф. Розенблатом в автомате, названном им «персептроном» (от слова «perception» - восприятие). Рассмотрим принцип действия автомата на примере пер-септрона МАРК-1 (рис. 11.27). В качестве воспринимающего устройства в персептроне использовано поле рецепторов в виде фотоэлектрического устройства, состоящего из нескольких сотен фотоэлементов. Каждый фотоэлемент может находиться в одном из двух состояний: О и 1. Выходные сигналы фотоэлементов поступают на входы «ассоциативных элементов» А, число которых сравнимо с числом фотоэлементов. Каждый Л- элемент имеет несколько входов и один выход. Входы Л-элементов соединяются с выходами фотоэлементов случайным образом и со случайными знаками. В процессе обучения случайные связи сохраняются неизменными. Л-элементы осуществляют алгебраическое суммирование поданных на их входы сигналов с фотоэлементов и сравнивают получаемую сумму с постоянным числом Q в соответствии с алгоритмом где = 1 при;г,х,- (3J>0; о при / V г,Х-qWo, \г=1 / -f 1 при подключении /Л-элемента со знаком « + »; - 1 при подключении /Л-элемента со знаком « -»; о при неподключенном /Л-элементе. 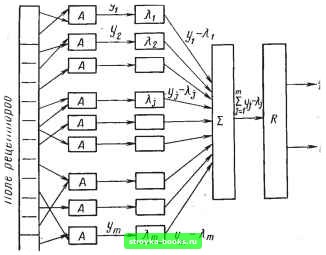
о Рис. 11.28 Выходные сигналы Л-элементов после перемножения на независимые переменные коэффициенты складываются (рис. 11.28) y==hyi (11.232) и поступают на вход реагирующего элемента R, который может находиться в одном из двух состояний: или О, или 1 в зависимости от положительности суммы (11.232), т. е. 1 при 2 hyi>\ О при 2 hyj<.-/=1 (11.233) В процессе обучения персептрон должен вьщавать выходной сигнал О при предъявлении объектов класса А и выдавать сигнал 1 при предъявлении объектов класса В. Обучение заключается в том, что коэффициенты kj при каждом показе объектов класса А и получении на выходе Л-элементов сигналов 1 увеличиваются на некоторую величину, а при отказе объектов класса В уменьшаются на эту величину. Постепенно правильность ответов на предъявляемые объекты увеличивается, так как повышается сумма (11.232) при правильной классификации. По окончании обучения на последовательности объектов конечной длины автомат распознает с определенной точностью объекты классов Ли В, если они и не предъявлялись ему на этапе обучения. Схема обучения представлена на рис. 11.28. Решающее правило выглядит следующим образом: Rf (X, Я*)= 2 ё" 2 iiXi-Q У = 1 \/=1 (11.234) [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [ 155 ] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |