
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [ 15 ] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 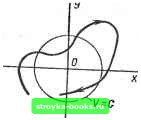 Рис. 7.38 которое в этом случае является точкой асимптотически устойчивого равновесия. Задача о нахождении функции Ляпунова, которая для данной системы дала бы необходимое и достаточное условие устойчивости, весьма сложна и практически пока неразрешима. В зависимости от конфигурации фазовых траекторий уравнение замкнутой поверхности V = С, которая при всех С пронизывалась бы траекториями только снаружи внутрь или наоборот, найти весьма трудно. Поэтому при отыскании функции Ляпунова им обычно заранее приписывают некоторую форму, параметры которой сравнительно несложно вычисляются по исходным уравнениям движения. Если функцию заданной формы при этом найти удалось, можно быть уверенным, что равновесие устойчиво. Если же это не удалось, это еще не означает, что равновесие неустойчиво, может просто оказаться, что функции Ляпунова данной формы не существует, но существует функция другого вида. Так, если фазовые траектории имеют вид, показанный на рис. 7.38, и будем искать функцию Ляпунова в виде сферы V = = Xi, то это вряд ли удастся, так как траекторий всегда бу- дут в некоторых точках входить в сферу, а в некоторых - выходить из нее, хотя равновесие устойчиво. Для линейных систем функции Ляпунова представляют собой квадратичные формы координат, координаты которых находится сравнительно несложно. Задаемся квадратичной формой с неопределенными коэффициентами k. г=1 и находим коэффициенты , из условия dV/dt 2 dVldxydxjldt==- А i= 1 (7.49) (7.50) где Л -любая постоянная. Подставляя в (7.50) выражения dXildt из исходных уравнений движения и выражения dV/dx,-, из продифференцированного уравнения (7.49), сравниваем ко- эффициенты при одинаковых членах в левой и правой частях и получаем алгебраические уравнения дпя нахождения коэффициентов а,. Иногда функцию Ляпунова в виде квадратичной формы удается отыскать и для нелинейных систем, близких к линейным, но вообще такое ограничение формы резко сужает возможности исследования. Довольно существенное расширение возможностей дает форма функции Ляпунова, предложенная А. И. Лурье и В. И. Постниковым. Если нелинейность обусловлена введением в линейную систему одного безынерционного нелинейного звена со статической характеристикой = ф (а), принадлежащей классу (О, К), то функцию Ляпунова во многих случаях удается построить в виде «интеграл от непинейно-сти плюс квадратичная форма»: VR(x) + bff(l)dl, (7.51) где квадратичная форма R (х) имеет вид /?(х)=х*Нх, при этом X* - матрица-строка, полученная транспонированием вектора х, а Н - квадратная определенно положительная симметрическая матрица типа п X п, элементы которой постоянны и рассматриваются как искомые неопределенные коэффициенты. § 7.10. Абсолютная устойчивость Рассмотрим свободное движение в системе, состоящей из линейной части с передаточной функцией W (в) и нелинейной отрицательной обратной связи с характеристикой = ф (а) (рис. 7.39). Уравнения для этой схемы можно записать в виде o=-W(s)l;l4>(о); Ф(0) =-0. (7.52) Уравнения для линейной части записаны для изображений Лапласа а и переменных а и . Условие ф (0) = О, наложенное на функцию ф (), означает, что в точке а = О, = О система имеет состояние равновесия: пара а = 0; =0 является тривиальным решением дифференциальных уравнений (7.52). Мы будем исследовать условия устойчивости этого состояния равновесия, т. е. устойчивость тривиального решения. Уравнения (7.52) можно записать также в переменных состояния: "" 1д/5 x=Ax-fb; = ф(а); а=сх, (7.53) где X - п-мер ный вектор состояния; д - постоянная (п X п)-матрица; с - постоянный (п X 1)-вектор; b - по- 9() стоянный (п X 1)-вектор. Между передаточной функцией W (s) и коэффициентами уравнений (7.53) существует зависимость Рис. 7.39 lF(s)=c(А-sE)-b, (7.54) где Е - единичная матрица. Передаточная функция W (s) для уравнения (7 53) в общем случае равна отношению полиномов: IF (s) = М (s)/D (s). где степень полинома D (s) равна числу переменных состояния п. Равенство степени полинома D (s) числу переменных состояния п существенно - это означает, что передаточная функция W (s) невырождена, т. е. М (s) и D (s) не имеют одинаковых множителей вида s - При этом условии система (7.53) полностью управляема и эквивалентна системе (7.52). Степень полинома М (s) вообще равна п- 1, но при некоторых значениях коэффициентов ац матрицы А может быть и меньше, вплоть до нуля. Если уравнения состояния имеют вид X = Ах -Ь Ь; I = ф (а); а = с х + ql. (7.55) где q - отличное от нуля постоянное число, то степень М (s) равна степени D (s). Важной особенностью общей теории устойчивости нелинейных систем указанного вида является то, что рассматриваются не конкретные виды функций ф (•) (т. е. не параболы, экспоненты и т. п.), а классы функций, удовлетворяющих тем или иным ограничениям. Если положение равновесия системы (7.53) или (7.55) асимптотически устойчиво в целом при любой нелинейной функции ф (•) из заданного класса, то она называется абсолютно устойчивой в этом классе. Мы будем рассматривать класс функций ф (•), удовлетворяющих секторным ограничениям. Их характеристики = ф (а), построенные в плос- [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [ 15 ] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0016 |