
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [ 18 ] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] Это неравенство определяет область, в которой должны располагаться частотные характеристики W (/ш) линейной части для того, чтобы нелинейная система из класса {Ки Kz) была абсолютно устойчивой. Границу этой области получим, заменив в (7.74) знак неравенства на знак равенства. Это будет уравнение окружности с центром на вещественной оси в точке --Y (-\- т)" проходящей через точки - l/Ki и - I/K2 на оси Р. Неравенство (7.75) требует, чтобы частотная характеристика располагалась вне круга, ограниченного этой окружностью. На рис. 7.40 слева построены запретные области (заштрихованные) для характеристик ф (о) для разных W(jw)     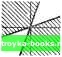 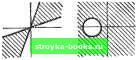 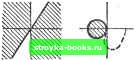 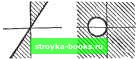 значений /i и /Сз и справа от них - соответствующие запретные области лля частотных характеристик W (/со). Для нелинейностей из подкласса (О, К) окружность вырождается в прямую, проходящую через точку - \1К на оси Р, параллельную оси jQ. Для нелинейностей из подкласса (О, оо) окружность вырождается в мнимую ось и внутренность круга перейдет в правую полуплоскость. Заметим, что круговой критерий справедлив и для нестационарных характеристик = ф (/, о), если только они при любом t не выходят за пределы данного сектора. В этом отношении критерий является весьма сильным. Но он обычно дает
        слишком большую избыточность. Для стационарных характеристик, принадлежащих классу (О, /С), значительно меньшую избыточность дает частотный критерий В. М. Попова. Критерий В. М. Попова. Нелинейные характеристики из класса (О, К), как стационарные, так и нестационарные, как было показано, удовлетворяют локальной связи (7.59) FAl, а) = {Ка-1)1>0. (7.76) Стационарные характеристики из того же класса удовлетворяют еще интегральной квадратичной связи по переменным 5 и а. . . Обозначим Г . 0(a)=f(p(a)da.; [ (7.77) о . Так как ф (о) > О, то Ф (о) >0. Поэтому, полагая • для I = ф (о); о = о {t) имеем •• • • . J f, (g (/), о (./)1 dt = "j ф [О (01 da(f) = • • о а(0) =Ф[о(0]-Ф1а(0)]>-Ф[а(0)]. (7.78) Таким образом, стационарная характеристика ф (сг) из класса (О, К) удовлетворяет локальной связи с формой f, и интегральной связи с формой f 2. Составим форму: -j ... Fa,a,o)FAl,a). + i}F.Al, а), -(7.79) где :&:>0 - некоторое вещественное положительное число. Форма (7.79) удовлетворяет интегральной связи вида (7.58). f {f [I (t), a (t), a m dt >-m [a (0)]. Найдем расширение формы F до эрмитовой. Расширение формы Fi даио соотношением (7.69). Расширение формы F = , ?2 = Re а 1* - Re [-j(i>W (/со)] I \\ Тогда получаем ?(Mf) = -Re[l + /CU?(/co)-h/««W7(/»)]iP. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [ 18 ] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0014 |