
 |
|
Главная Нелинейные системы управления [0] [ 1 ] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] связи находится непосредственно из характерисги1си /: х = Оа. Но при наличии отрицательной обратной связи отрезок Оа будет равен результирующему входному воздействию: Оа ~ =Хвх-ф (вых). гдеф (Хв„„) - характеристика обратной связи. Поэтому для нахождения х к Оа надо прибавить величину воздействия обратной связи: х = Оа + ср (Хв„). Если во втором квадранте построить характеристику обратной связи х. = ф (Хвых), направив ось Хо.с влево, то величина хх будет равна сумме отрезков Оа и Ob, т. е. расстоянию от точки 2 до точки Перенеся этот отрезок измерителем по горизонтали вправо так, чтобы левый конец отрезка лег на ось ординат, получим точку 3 результирующей статической характеристики. При положительной обратной связи Хвх=Ш- ф (Хвых) характеристику удобнее строить в первом квадранте, совместив ось Хо-с с осью Хвх (рис. 7.5, в). Искомая абсцисса Ос результирующей характеристики / равна разности: Ос - = Оа - Ob, т. е. расстоянию Ьа между кривыми / и . Если же между нелинейными звеньями имеются разделяющие их инерционные линейные, то систему уже не удается свести к рассматриваемому классу. Она относится к классу систем с несколькими нелинейностями, в данной книге не рассматриваемому. Если передаточная функция линейной части равна IF (s) = = М {s)/N (s), а уравнение нелинейного элемента имеет вид У = (р (х), то дифференциальные уравнения системы Nip)x = M{p){f--yy, где р = d/dt, или N(p)x+ М (р) ф (X) - М (р) f. Часто систему приводят к виду Х(/Л= 2 (iis + bj, i= 1, 2, п; Хп = ф И; 0 = 2 C;Xj. (7.1а) (7.16) (7.1 в) Так, например, описывается система регулирования с сервомотором, имеющим нелинейную характеристку ф (а). Сервомотор воздействует на одну из координат х„, его входная величина о в общем случае есть линейная функция остальных координат. В частном случае, когда все Сг, кроме одного, равны нулю, уравнения (7.1 в) переходят в уравнения (7.16). Некоторые наиболее распространенные типы нелинейных характеристик показаны на рис. 7.6. Характеристика / свойственна системам с насыщением, характеристика 2 - электромагнитным устройствам с гистерезисом, характеристика 3 - выпрямителям. В практике часто встречаются элементы, характеристики которых кусочно-линейны или аппроксимируются кусочно-линейными графиками. Кривая 4 изображает кусочно-линейную аппроксимацию кривой намагничивания, кривая 5 - характеристики с насыщением, кривая 6 - характеристики идеального выпрямителя. Кусочно-линейными характеристиками обладают: идеальное поляризованное реле (кривая 7), трехпо-зиционное поляризованное реле с зоной нечувствительности (S), трехпозиционное реле с зоной нечувствительности и гистерезисом (5), у которого величина срабатывания Оа больше величины отпускания Ос, двухпозиционное реле с гистерези-  -а-с
о к о 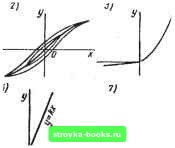 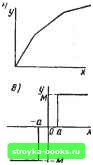 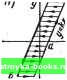 А 12) У X -а-с с а X Рис. 7.6 com (10), например поляризованное реле, которое не имеет устойчивого, отключенного состояния и контакт которого всегда замкнут в ту или другую сторону. Механизмы с мертвым ходом имеют характеристику, изображенную кривой 11. При сцеплении передач перемещение ведомой шестерни происходит в одну сторону по линии А, в противоположную - по линии Б. При изменении направления движения, пока выбирается мертвый ход, ведомая шестерня неподвижна (горизонтальные участки). Сходную характеристику имеют и элементы с сухим трением, если по оси х откладывается прилагаемое к подвижной части усилие, а по оси у - ее перемещение. Кривая 12 изображает характеристику нейтрального э.пектромагнитного реле с гистерезисом. Для последующего изложения полезно в рассматриваемом классе нелинейных систем выделить подкласс (О, оо), у которого характеристика ф (х) проходит через начало координат и укладывается в прямых углах, образованных осями хну и лежащих в первом и третьем квадрантах. Поскольку первая ось. имеет угловой коэффициент О, а вторая оо, введено обозначение подкласса (О, оо). Внутри угла характеристики могут располагаться произвольно, сколь угодно близко подходить к сторонам угла и частично с ними совпадать. К этому подклассу относятся кривые 1, 3, 4, 5, 6, 7, 8 и 9. Внутри подкласса (О, оо) иногда выделяют более узкий подкласс (О, /С), у которого характеристики лежат в острых углах, образованных осью X и проходящим через начало координат лучом с угловым коэф фициентом /С, лежащим в первом и третьем квадрантах. К данному подклассу относятся характеристики 1, 3, 4, 5, 6, 8 и 9 Характеристики 2, 10, 11 и 12 к отмеченным подклассам не относятся. § 1.2. Изображение движений в фазовой плоскости Когда движение можно описать координатами хну посред-етвок уравнений dxJdt = /i (x, у) и dyldt = /2 i, у), то для исследования часто оказывается удобно изобразить движение на плоскости в прямоукольной- системе координат х и у. Координаты X и ув этом случае называют фазовыми координатами, время t в явном виде в изображение движения не входит. Косвенно оно отражается так: каждому моменту t н СООТВСТСТ" [0] [ 1 ] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0014 |
|||||||||||||||||||||||||||||||