
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [ 20 ] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 5. Приведем без доказательства алгоритм проверки условия В. М. Попова (12). Построим полином I det (А -/wE) 1" {/С-Ч- Re [(I + /сот) J (А- /соЕ)-» Ь]} = где п - степень характеристического полинома линейной части. Составим таблицу. соп ( l)np(„ ,,( l)«-ip .......-ЯгРо (-1)"2пРгп (-1)"-»2 (я-1) Ра (п-1) . . .-22 (-1)"--72(„ .,.............о 0)0= I Первые две строки таблицы образованы из коэффициентов полинома Р (/(О) (первая строка) и из производных dP (/(u)/d(o (вторая строка). Элементы остальных строк вычисляются по правилу составления таблицы Рауса, приведенному в первой части*. Если элементы первого столбца данной таблицы удовлетворяют условию Ли-П-Ргп. (-1)"2пЯ2„ Яо] = л. Я2п>0. (7.83) где N - число перемен знаков в той последовательности, которая заключена в (7.83) в квадратные скобки, то условие Попова (7.80) выполняется при всех со. Гипотезы М. Айзермана и Р. Калмана. Устойчивость в гур-вицевом угле. Заменим в системе (7.52) нелинейный элемент линейной отрицательной обратной связью: ? = - txo. (7.84) Тогда образуется линейная замкнутая система, характеристический полином которой будет D (S) -f jxM (s), (7.85) где М. (s) - числитель, а D (s) - знаменатель передаточной функции Л4 (s). * Для вычисления данной таблицы удобно пользоваться правилом Рауса в следующей формулировке: каждая строка таблицы начиная с третьей получается из двух предыдущих строк вычитанием из первой строки второй, умноженной на отношение элементов первой из этих двух строк и второй, стоящих в первом столбце. Затем полученная строка сдвигается иа один шаг влево. Эту систему называют системой сравнения. Пусть при выполнении неравенства Im < < fA( (7.86) полином (7.85) гурвицев, т. е замкнутая линейная система устойчива. Наименьшее р,,„ и наибольшее значения [х, при которых система попадает на границу устойчивости, ограничивают угол ([i-m, 1м). называемый гурвицевым углом. В процессе развития теории абсолютной устойчивости были высказаны две гипотезы. Гипотеза М. Айзермана. Пусть даны уравнения (7.53), нелинейность принадлежит сектору (Ki, Кг) и для всех К б (kj, /Сг) матрица А + Ьс/С гурвицева. Тогда нелинейная система абсолютно устойчива. Иными словами, по гипотезе М. Айзермана, угол (/Ci. Кг) равен гурвицеву углу (fA,„, ц), т. е. система абсолютно устойчива в гурвицевом угле. Гипотеза оказалась в общем случае неверной (для нее был указан противоречащий пример). Тогда была выдвинута гипотеза Р. Калмана. Гипотеза Р. Калмана. Пусть в уравнениях (7.53) нелинейность удовлетворяет условиям < /Сз (7.87) и для всех К € (Kl, Кг) матрица А + Ьс/С гурвицева. Тогда нелинейная система абсолютно устойчива. Гипотеза оказалась неверной в общем случае. Но для многих видов передаточных функций линейных частей гипотезы либо М. Айзермана, либо Р. Калмана могут выполняться. Отыскание условий, при которых выполняются эти гипотезы, представляют существенный интерес для практики, так как абсолютная устойчивость нелинейных систем, для которых гипотезы выполняются, может исследоваться по линейным критериям. Можно сказать, что такие системы абсолютно устойчивы, если они минимально устойчивы. Представим частотную характеристику W (/со) линейной части в виде Wii(o) = KoWoiKo); Го(0) = 1, где Ко - передаточный коэффициент линейной части; Wq (/to)- «нормированная» частотная характеристика с передаточным коэффициентом, равным единице. Выберем Ко достаточно малым так, чтобы характеристика W (/со), а следовательно, и (/со) располагались правее прямой Р = - ПК (рис. 7.42). Пусть характеристика пересекает отрицательную вещественную полуось и крайняя левая (т. е. наиболее удаленная от начала координат) точка пересечения соответствует частоте со. Пусть частотная характеристика W" (/со) такова, что касательная к ней в точке, соответствующей со = ф;,, не имеет пересечений с кривой, т. е. характеристика W (/oi) лежит правее этой касательной, как показано на рис. 7.42. Назовем касательную MN, правее которой расположена кривая, предельной касательной. Проведем через точку - \/К на вещественной оси прямую, параллельную предельной касательной. Очевидно, что для нелинейностей из сектора (О, К) эта прямая будет также прямой Попова. Начнем увеличивать Кс- Тогда размер характеристики будет увеличиваться, но форма ее будет сохраняться и предельная касательная будет перемещаться влево параллельно самой себе (пунктирные кривая и касательная на рисунке). Когда Ко достигнет такой величины, что левая точка пересечения характеристики попадет в точку - l/K на вещественной оси, будет иметь место равенство Коо (озц) =; = - 1/К, т. е. KoKWo (со,,) = 1. Кривая Найквиста разомкнутой системы КоК Woija), таким образом, пройдет через критическую точку -1, О и устойчивость линейной замкнутой системы нарушится. Но одновременно и предельная касательная совпадет с прямой Попова и нарушится условие Попова для абсолютной устойчивости нелинейной системы из класса (О, К)- В данном случае верхняя граница гурвицева угла совпадает с углом (О, К). Нижняя граница, правда, не совпадает, но нас она не интересует, поэтому мы назовем данную систему абсолютно устойчивой в гурвицевом угле. Гипотеза М. Айзермана для нее справедлива в положительной части гурвицева угла. Пусть теперь характеристика W" (/ш) такова, что предельная касательная MN к ней не проходит через крайнюю левую точку пересечения характеристики с отрицатель ной вещественной полуосью (рис. 7.43). В процессе возрастания Ко при некотором его Рнс. 7.42 значении Koi предельная ка- 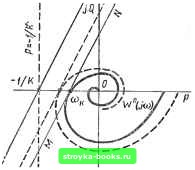 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [ 20 ] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0014 |