
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [ 21 ] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 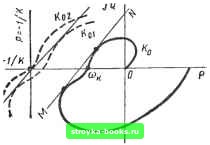 Рис. 7.43 сательная совместится с прямой Попова и условие Попова для абсолютной устойчивости нарушится, хотя линейная замкнутая система с тем же значением К01 будет еще устойчивой. Нарушение ее устойчивости произойдет при значении Koz > Кои когда точка, соответствующая со = ft) к частотной характеристике, попадет в точку- 1/К- Система с такой характеристикой W (/со) не будет абсолютно устойчивой в гурвицевом угле, и для нее несправедливы ни гипотеза М. Айзермана, ни гипотеза Р. Калмана. С помощью описанных построений можно в плоскости (сг,ф) построить секторы абсолютной устойчивости Sy, асболютной неустойчивости S„ и неопределенности. Вещественная ось и прямая Ь, = KoiO ограничивают в первом квадранте сектор абсолютной устойчивости 5у (рис. 7.44). Прямая g = Ког является нижней границей сектора абсолютной неустойчивости Sh (заштрихован однократно), в котором линейная система неустойчива и не соблюдены условия Попова. Между прямыми I = KoiO и I = KoiO заключен сектор неопределенности, в котором линейная система сравнения устойчива, но достаточное условие абсолютной устойчивости не соблюдается и мы не можем утверждать, что система абсолютно устойчива, но и не можем сказать, что она неустойчива. Графоаналитический метод позволяет легко определить, будет ли система абсолютно устойчивой в гурвицевом угле (или его положительном секторе), но аналитическое определение этого весьма сложно. В настоящее время установлено, что нелинейная система из класса (О, К) устойчива в гурвицевом угле, если линейная часть состоит из любого числа последовательно включенных устойчивых звеньев первого порядка. В случае дифференцируемых монотонно возрастающих нелинейных характеристик из класса (О, К), одновременно удовлетворяющих неравенствам О <d(p/da < К, линейная часть может кроме упомянутых звеньев первого порядка иметь в последовательной цепи любое число колебательных звеньев, передаточные функции которых имеют комплексные полюсы 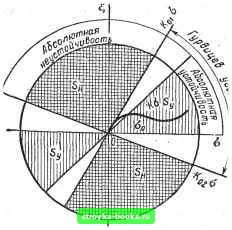 Рис. 7.44 С отношением мнимой части к вещественной, не превышающим КЗ [5]. Определение автоколебаний. Обычно при приближенном определении автоколебаний исходят из предположения, что существует периодическое решение исходного дифференциального нелинейного уравнения. В системах второго порядка, как следует из теоремы Бендик-сона, действительно, автоколебания, если они существуют, будут периодическими. Но в системах более высокого порядка возможно существование непериодических незатухающих колебаний, которые могут и не обнаружить метод гармонического баланса и другие методы, основывающиеся на предположении существования периодического решения. В ряде случаев частотные методы исследования абсолютной устойчивости и неустойчивости позволяют найти условия возникновения не только периодических автоколебаний, но и незатухающих непериодических колебаний. Расширим понятие автоколебаний на непериодические незатухающие колебания. Пусть заданы два вещественных числа: а<0 и Р>0. Решение X (t) называется (а, Р)-колебательным по выходу о (t), если при сю выполняются условия: а) \х (01 < const; б) точка о (О бесконечно много раз находится в каждом из интервалов (-оо, а), (Р, оо) и, следовательно, в интервале [а, р]. Если при этом время пребывания точки о (f) в каждом из интервалов (~-оо, а), (Р, оо) и (а. Р) (без выходов из него) ограничено некоторой постоянной Т > 6, то колебание называется нерастягивающимся. Если указанные свойства справедливы и. при t- .- оо, то колебание, называется двусторонним.- . ; -ни • Двусторонние нерастягивающиеся колебания называются автоколебаниями. Упрощенный критерий колебательности. Рассмотрим систему . . Сделаем допущения: 1) передаточная функция невырождена; 2) система имеет единственное стационарное состояние g = О, о = О, т. е. прямая о -- В? (0)g = О пересекается с графиком нелинейности ф (о) только в начале координат, если det А =7 О, и с прямой g = О, если det А = 0; 3) существует производная ф (0), функция ф (о) кусочно-непрерывна, линеаризованная в нуле система (т. е. система с обратной связью = - ф (0) о) не имеет периодических решений; 4) существует предел um -s-=a<xi. Пусть для рассматриваемой системы построены секторы абсолютной устойчивости и абсолютной неустойчивости. Тогда: - если график нелинейности ф (о) целиком расположен в секторе устойчивости Sy, то система устойчива в целом; -- если график ф (о) расположен целиком в секторе неустойчивости S„, то система неустойчива в целом; - если график ф (о) при \о\ < лежит в секторе неустойчивости S, а при а > 0, кривая ф (о) входит в сектор устойчивости и остается там, вокруг точки о = О возникают автоколебания [кривая ф (о) на рис. 7.441. При этом числа а, р определяются как абсциссы точек пересечения характеристики ф (а) с лучами, ограничивающими секторы неустойчивости в верхней и нижней полуплоскостях. Определение границ секторов абсолютной устойчивости и неустойчивости выше иллюстрировалось на примере, где нелинейность принадлежит сектору (О, К), и использовался критерий Попова. При нелинейностях из другого класса используются другие соответствующие частотные критерии. Числа а и Р являются нижними оценками размаха колебаний, истинная величина размаха может быть больше. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [ 21 ] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0014 |