сигнала: входное воздействие х (t) и некоторый постоянный сигнал

Xq = aja.

Величина кванта нелинейного элемента

А = 2л/а.

(8.10)

(8.11)

Таким образом, на выходе модулятора (рис. 8.6) получается последовательность прямоугольных импульсов длительностью у; амплитуда импульсов определяется величиной вертикальной ступени характеристики Н Э, а моменты их появления определяются уравнением (8.9).

Выше рассмотрены уравнения и структурная схема одно-полярной ЧИМ, которая достаточно широко распространена в системах связи. Как указывалось выше, в системах автоматического управления удобнее двухполярная ЧИМ. Структурную схему для такого ЧИ-модулятора достаточно легко полу-чтъ,, используя схему однополярного ЧИ-модулятора.

Действительно, если положить Хо = О и предположить, что полярность выходных импульсов определяется полярностью входного сигнала х, то уравнение (8.9) с учетом обозначения (8.11) можно привести к виду

Здесь ср (4) = ф (4)/а.

(8.12)

Формирователь I-

Рис. 8.7

Ha интервале одного периода импульсной последовательности tn - „-1 уравнение (8.12) запишется в виде

± J" х(ОЛ = ±А. (8.13)

Структурная схема двухполярного ЧИ-модулятора, построенная согласно уравнению (8.13), приведена на рис. 8.7. В отличие от схемы рис. 8.6 в ней отсутствует сумматор, а нелинейный элемент квантования представлен гистерезисной характеристикой, у которой нижняя ветвь определяет формирование импульсов положительной полярности, а верхняя - отрицательной.

Нелинейный элемент квантования приращений (рис. 8.8,а) обладает характеристикой, имеющей ряд общих моментов с характеристикой квантования по уровню. Принципиальное отличие состоит в том, что у характеристики квантования при-

б) У

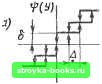y-y(to)

значения по

У"

н.э. г.

и. Э-1. Формирователь Рис. 8.9

ращений

оси абсцисс соответствуют не текущей величине входного сигнала у, а разности его со значением у (to) входного сигнала в момент to начала . преобразования. На рис. 8.8, б иллюстрируется во времени процесс преобразования сигнала у (t) нелинейным звеном. Выходная величина т)? (t) представляет собой ступенчатую функцию, моменты переключения которой совпадают с моментами определения переменного параметра импульсной последовательности. В настоящее время термин двухтактная или двухполярная ЧИМ практически не употребляется. Модуляция, определяемая уравнением (8.13), называется интегральной ЧИМ (ИЧИМ).

Структурная схема широтно-импульсного модулятора. Для построения структурной схемы ШИ-модулятора удобно использовать геометрическую интерпретацию, примененную при построении структурной схемы ЧИ-модулятора.

При ШИМ производится управление фазой вектора и (t) (см. рис. 8.5) в линейной зависимости от входного воздействия X (t). Таким образом, уравнения (8.5), (8.7), (8.8) дополняются при ШИМ уравнением вида

(t) (Оо (t) + ах (t). (8.14)

Решив совместно уравнения (8.5), (8.7), (8.8), (8.14) с учетом (8.11), получаем соотношение для определения момента t„ появления модулируемого фронта импульса:

«6п+х(0=-Ап+ф(д. (8.15)

где соб - частота следования импульсной последовательности.

В соответствии с геометрической интерпретацией ШИМ и уравнением (8.15) структурная схема ШИ-модулятора построена на рис. 8.9. Она представляет собой последовательное соединение сумматора, на вход которого подаются сигналы х (t) и <о6 (t), нелинейного элемента квантования приращений (Н.Э1) и формирователя импульсов, который в данном случае выполнен в виде сумматора, на один вход которого подается сигнал с выхода НЭ1, а на другой-сигнал с аналогичного нелинейного элемента НЭ2 (рис. 8.9).