
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [ 29 ] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 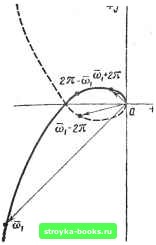 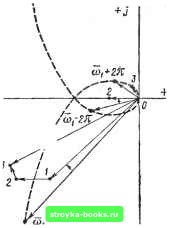 Рис. 8.13 Рис. 8.14 Данную величину удобно определять по таблицам . По- вернем соответствующий вектор на угол со, -f 2лк 5) суммируя построенные векторы и умножая сумму на величину -уо. определяем согласно (8.37) значение W* (/©i) частотной характеристики разомкнутой системы на частоте coj. На рис. 8.14 процесс построения поясняется на примере точек, соответствующих частотам (Oj, - 2л, щ + 2л. Цифрами 1, 2, 3 обозначаем векторы, преобразованные согласно п. 4 порядка построения. Сумма этих векторов с точностью до коэффициента Yo определяет вектор W* (/coj). Далее аналогично строят точки частотной характеристики на других частотах (©2, Юз.---) из диапазона О < « < л. Соединяя построенные точки, получаем годограф W* (/со). Во многих случаях при достаточно больших значениях со значение \W* (/«) существенно уменьшается, поэтому в выражении (8.37) можно ограничиться двумя слагаемыми для упрощенного приближенного вычисления W* (/«): tt7(/to)--e + (0 -2л + [/(«-2я)1- •Yo / 0) -2jt Vo (8.38) Порядок построения W* (/«) no выражениям (8.38) иллюстрируется на рис. 8.15. На рис. 8.15, а показаны векторы W{i(Oi), W Jja), а также векторы W (/я), W (/ (2п - щ)], W [j (2я- - соа)! и им сопряженные. На рис. 8.15, б у этих векторов уменьшены модули, изменены фазы и произведено суммирование согласно (8.38). Для того чтобы не перестраивать кривую W (/со), изменяя ее в Vo раз, можно изменить масштаб по действительной и мнимой осям в Vo раз. Из соотношения (8.38), а также из общего выражения (8.37) достаточно очевидно, что при со = я конец вектора W* (jn) всегда лежит на действи- 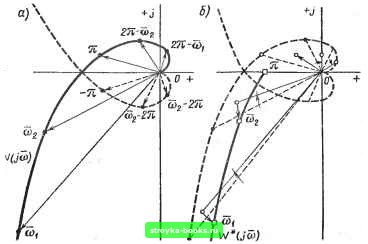 тельной оси, поскольку Im W* (/я) = 0. Известны и другие способы построения W* (/и), которые достаточно подробно описаны б работах [1,5]. Исследование устойчивости систем с амплитудно-импульсной модуляцией. Пусть решетчатая функция х [п] представлена в виде вынужденной и свободной составляющих, т. е. определяется выражением вида х[п1=Хв[п]-Хсв[п1 (8-39) Вынужденная составляющая процесса х In] определяется видом внешнего воздействия. Свободная составляющая характеризует отклонение процесса х (п) от вынужденной составляющей Хв [п] и определяет переходный процесс. Она может быть представлена в виде х,Ап]= i:d,ei\ (8.40) £= 1 где di - некоторые коэффициенты; qi - основные полюсы передаточной функции замкнутой импульсной системы, т. е. основные корни характеристического уравнения вида G* (q) = 1 4- W* (9) = 0. (8.41) Основными будет считать корни, расположенные в полосе - - я<С Im<: я, поскольку все остальные корни отличаются от них на величину ± /2ят. Если W* (q) представить в виде W*{q)-P*{q)lQU.q), то характеристическое уравнение замкнутой системы можно записать в виде G*{q)-Q*iQ) + P4q)0. (8.42) Если с течением времени Хсв 1"! стремится к нулю, т. е. Итх,в[п]=0, (8.43) д-*.оо то импульсная система называется устойчивой. Если с течением времени Хсв 1«1 неограниченно возрастает, т. е. Итл;св[п] = оо, , (8.44) , П-»-оо то импульсная система называется неустойчивой. В промежуточном случае, когда Хсв tnl с течением времени не стремится к нулю и не возрастает неограниченно, импульсная система [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [ 29 ] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0012 |