
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [ 30 ] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] называется нейтральной. В устойчивой системе процесс х {п) с течением времени стремится к вынужденной составляющей. Анализ выражения (8.40) с достаточной очевидностью показывает, что если все основные полюсы qt имеют отрицательные вещественные части, то при п- оо все слагаемые (8.40) стремятся к нулю и, следовательно, выполняется условие (8.43), соответствующее устойчивой импульсной системе. Если хотя бы один из полюсов Qi имеет положительную вещественную часть, то соответствующее слагаемое в (8.40) неограниченно возрастает и, следовательно, выполняется условие (8.44), соответствующее неустойчивой импульсной системе. Наконец, если хотя бы один из полюсов q; имеет вещественную часть, равную О, а все остальные полюсы - отрицательные вещест- венные части, то выполняется условие, соответствующее нейтральной системе. Таким образом, для того чтобы импульсная система была устойчива, необходимо и достаточно, чтобы все полюсы ее передаточной функции имели отрицательные вещественные части или чтобы все эти полюсы лежали в лети части полосы - л <: Im 9 < л комплексной плоскости q (рис. 8.16). Так как основные полюсы W* ((?) совпадают с полюсами W (q), то устойчивость линейной части системы обеспечивает устойчивость разомкнутой импульсной системы. В общем случае вычисление корней qt является трудной и громоздкой задачей, однако для суждения об устойчивости нет необходимости определять сами корни, достаточно лишь установить, лежат ли все они в левой части полосы - зх < Im зх. Ответ на этот вопрос дают критерии устойчивости. Рассмотрим алгебраические и частотные критерии, аналогичные тем, которые использовались для анализа устойчивости линейных непрерывных систем. Алгебраический критерий устойчивости (аналог критерия Гурвица). Пусть характеристическое уравнение исследуемой замкнутой импульсной системы имеет вид G* (q) = о, е" + Q,, ес- > 9 + ... + Of,. (8.45) Произведем в характеристическом многочлене G* {q) замену переменных: Z = е". (8.46) Тогда получим G(z)=o,z--a,iz- + ... + ао- (8.47) 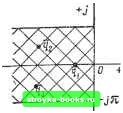 Плоскость 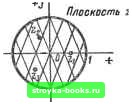 Рис. 8.16 Рис. 8.17 Так как подстановка (8.46) преобразует полуполосу - п <i <: Im <? < я. Re <7 < О (рис. 8.16) во внутренность круга единичного радиуса (рис. 8.17) z < 1, то применительно к плоскости Z необходимое и достаточное условие устойчивости формулируется следующим образом: замкнутая импульсная система устойчива, если все корни G {г) лежат внутри круга единичного радиуса, т. е. все нули G (г) по модулю меньШе единицы. Для того чтобы привести условия устойчивости импульсной системы к аналогичным условиям устойчивости Гурвица для непрерывных систем, в многочлене (8.47) произведем подстановку: f = (Z - l)/(z + I) или z = (1 + v)/{] - v), (8.48) тогда характеристический полином принимает вид • G(t.) = t-4 6, it-(-) + ... + 6o- (8.49) Плосиость гГ- Так как подстановка (8.48) преобразует круг единичного радиуса Б комплексной плоскости Z (рис. 8.17) в левую полуплоскость V (рис. 8.18), то условие устойчивости импульсной системы формулируется так: замкнутая импульсная система устойчива, если корни G (v) лежат в левой полуплоскости, т. е. если выполняются условия Гурвица bi>0, Ak>0, k= 1,2,..., /, где Afe -- определители Гурвица k-ro порядка (порядок вычисления их полностью совпадает с рассмотренным в гл. 3). 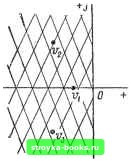 Частотный критерий устойчивости (аналог критерия Найквиста). Частотный критерий устойчивости импульсных систем, аналогичный известному из гл. 3 критерию устойчивости Найквиста для непрерывных систем, позволяет судить об устойчивости замкнутой системы по частотным характеристикам разомкнутой системы. Критерий Найквиста для непрерывных систем, как было показано в гл. 3, основан на принципе аргумента. Очевидно, что аналог принципа аргумента весьма несложно сформулировать и для импульсной системы, анализируя расположение корней, например, в плоскости z или плоскости V. Однако мы предлагаем это сделать читателю самостоятельно и ограничимся здесь лишь формулировкой критерия Найквиста для трех случаев, когда разомкнутая импульсная система устойчива, неустойчива и нейтральна. Если разомкнутая импульсная система устойчива (т. е. устойчива линейная часть системы), то замкнутая импульсная система регулирования устойчива, если годограф частотной характеристики разомкнутой системы при изменении а от О до п не охватывает точку (- 1, / О ). На рис. 8.19 изображены годографы W* (/со), соответствующие устойчивой (кривая /) и неустойчивой (кривая 2) системам. Если разомкнутая импульсная система неустойчива, т. е. если передаточная функция линейной части имеет г полюсов с положительной вещественной частью, то замкнутая система импульсного регулирования будет устойчива, если годограф W* (/со) частотной характеристики разомкнутой системы охватывает точку (- 1, / 0) е положительном направлении г 12 раз. Если разомкнутая система нейтральна, т. е. если передаточная функция содержит г полюсов, равных нулю, то импульсная система будет устойчива, если годограф W* (/со), дополненный дугой бесконечно большого радиуса, соответствуюией углу- - г я/2, не охватывает точку (- 1, / 0). На рис. 8.20 кривая / соответствует устойчивой, а кривая 2 - неустойчивой замкнутой системе. Частотную характеристику разомкнутой сис. темы W * (/со) можно построить, пользуясь выражениями (8.37), (8.38), или одним из способов, рекомендованных в [1,5]. Исследование качества систем с амплитудно-импульсной модуляцией. При исследовании качества систем автоматического управления возникают, как правило, три рода задач: 1) оценка установившегося значения сигнала ошибки системы [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [ 30 ] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0014 |