
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [ 31 ] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] Плоскость W*(jw) 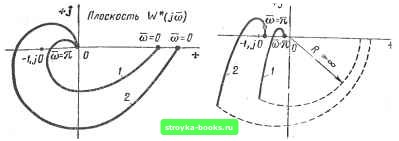 Рис. 8.19 Рис. 8.20 (установившееся значение отклонения входного сигнала импульсного элемента -х (см. рис. 8.12); 2) построение кривой переходного процесса в моменты съема t = п; 3) косвенная оценка параметров переходного процесса, в первую очередь оценка перерегулирования и времени регулирования. Рассмотрим задачу оценки установившегося сигнала ошибки системы. Сигнал на входе импульсного элемента и входной сигнал системы Хд (см. рис. 8.12) связаны соотношением (8.35): \+W* (<?) Хо(л). (8.50) Запишем передаточную функцию (8.35) в виде отношения двух многочленов Н* {q)/G* {q), где Н* {q) - многочлен степени l; G * {q) - характеристический многочлен степени /. Предположим, что Хд [п] имеет вид единичного скачка, т. е. Хд [П] 1 при п=0, 1,2,...; О при п< 0. Тогда сигнал х [п] в дискретные моменты времени будет определяться выражением х1п]-+ еЬ", (8.51)
Если система устойчива, то действительные части корней qi характеристического уравнения отрицательны и все слагаемые Б (8.51) с ростом п будут стремиться к нулю. Таким образом, X [ 00 ] = lim jc [п] = Я* (0)/G* (0) = 1 /(1 + IF* (0)]. (8.52) Значение (8.52) характеризует установившееся значение ошибки в системе с АИМ. Значение х [ оо] фО, если W* (0) ф Ф [оо], и обращается в нуль в астатической системе, т. е. в том случае, когда в контуре системы имеется интегрирующее звено (например, исполнительный элемент). Это несложно показать, если проанализировать соотношение (8.52) с учетом (8.32). Задачу построения кривой переходного процесса можно решить с помощью соотношения (8.51), однако данный подход весьма неудобен уже при степени характеристического уравнения / > 3, поскольку требует вычисления корней уравнения G*{q) =0. Рассмотрим предложенные в [1] более удобные способы, не требующие вычисления корней и позволяющие построить процесс при любом внешнем воздействии. Пусть передаточная функция замкнутой системы представлена в виде Разлагая ее в ряд по степеням е" и применяя обратное дискретное преобразование Лапласа, можно получить X {п\ = Хо [п -(/ ~h + (8.54) где коэффициенты r,j определяются из рекуррентного соотношения: (8.55) fcjj fe=0 при k>k; о, р, = 0 при [i>l. Выражение (8.54) позволяет определить процесс регулирования (для t = п) при любой форме [п]. Если Хо In] имеет вид единичного скачка, то Хо [п - (/ - + k)] равно единице при /г < п - / -Ь 4 и нулю при k> п - t Л- к, а значения процесса находятся суммированием коэффициента Г. ReW*Uo>)  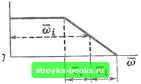 Рис. 8.21 Рис. 8.22 Второй способ построения кривой переходного процесса основан на использовании частотных характеристик. По известной W* (/to) строится вещественная частотная характеристика Re U* (/со). Если представить ее в виде суммы типовых трапецеидальных характеристик (рис. 8.21), то искомую величину Г,, можно выразить в виде sin (Ш к) ю1 k sin (Т; k) (8.56) Здесь Ai - площадь трапеции. Параметры произвольной t-й трапеции обозначены на рис. 8.22. Пользуясь таблицами -" , определяем Г,,, а затем по соотношению (8.54) строим кривую переходного процесса х [п]. Косвенные методы оценки показателей качества процесса регулирования в системах с АИМ играют такую же важную роль, как и в системах непрерывного регулирования. Рассмотрим следующие основные косвенные оценки: степень устойчивости, степень колебательности и интегральные оценки. Степенью устойчивости \ будем называть минимальную вещественную часть корня характеристического уравнения G*{q) = О замкнутой системы: I =min\Re9i\. (8.57) Так как исследуемые процессы выражаются в функции относительного времени / = п, то и степень устойчивости является относительной величиной. Примем обозначение для абсолютной величины степени устойчивости \, т. е. = %1Т. Для определения степени устойчивости достаточно в передаточную [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [ 31 ] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |