квантования no уровню. В практике систем автоматического управления получили достаточно широкое распространение так называемые системы с непрерывной передачей данных. Они применяются, в частности, в системах программного управления станками, в систе-Рис. 8.30 мах программного управления механиз-

мами прокатных станов и т. д. Если, оперировать структурной схемой, приведенной на рис. 8.29, то характерным признаком ЦС с непрерывной передачей данных можно считать отсутствие импульсного элемента в цепи рассогласования х {i). Если импульсная передача и применяется, то частота съема информации выбирается достаточно высокой, чтобы избежать потери информации и накопления ошибки. К системам с непрерывной передачей данных можно условно отнести и системы, у которых осуш,ествляется импульсная передача, но параметры импульсной системы соответствуют условиям ее эквивалентности непрерывной системе (условие эквивалентности рассматривалось в § 8.2). Эквивалентная структурная схема ЦС с непрерывной передачей данных представлена на рис. 8.30.Очевидно, что рассматриваемая система является нелинейной системой с нелинейным элементом квантования по уровню (см. рис-. 8.27). Для исследования данной системы можно использовать известные методы исследования нелинейных систем, рассмотренные в гл. 7. Для исследования абсолютной устойчивости ЦС с непрерывной передачей данных воспользуемся критерием абсолютной устойчивости нелинейных систем, приведенным в гл. 7: если замкнутая система состоит из устойчивой линейной части с передаточной функцией Wnn (s) (рис. 8.30) и нелинейности и характеристикой (л:), лежащей в угле О - < к, то достаточным условием устойчивости является выполнение неравенства

Re [(1 -f / pto) Wnn (/ю)! + l/fc > О, (8.71)

где р - произвольное вещественное число. :

В случае рассматриваемой ЦС /г = б /(0,5 Д) = 26/Д. Критерию абсолютной устойчивости можно дать удобную геометрическую интерпретацию, введя понятие модифицированной частотной характеристики Wj (/to), где

и<) =Re ir„„ (/со) -f /ю Jm (jo).

в этом случае критерий формулируется следующим образом: ЦС с непрерывной передачей данных успюйчива, если при устойчивой линейной части через т6чку{-А/{2Ь); /0) можно провести прямую так, чтобы годограф Wj (/to) лежал справа от нее.

Если достаточные условия абсолютной устойчивости для ЦС не выполняются, то в ней могут возникнуть периодические процессы. Исследование перирдических процессов можно выполнить с помощью метода гарюнического баланса. Будем полагать, что внешнее воздействие на систему отсутствует, и тогда условие существования периодического режима (в предположении, что приведенная непрерывная часть удовлетворяет гипотезе фильтра) можно записать в виде

И„э(4)„„(/(о)=.-1, (8.72)

где V/as(,A) - комплексный коэ4>фициент усиления нелинейного элемента квантования по уровню.

Уравнение (8.72) удобно решать графически, переписав его в виде

in„{/«)= ~Г,7,Ч)- (8-73)

Если уравнение (8.72) или (8.73) HilieeT решение, то в исследуемой ЦС существуют периодические колебания вида х {t) = -А sin (ct. Построив в общей системе координат годограф W х X (/to) и инверсную характеристику комплексного коэффициента усиления нелинейного элемента квантования - Wb [А), определим параметры колебаний Л, с» в точках пересечения данных характеристик. Аналитическое (выражение комплексного коэффициента (Л) можно записать в виде [91

Инэ (4) - i К4Лр(2ПЛ?, (8.74)

где/г - число ступеней характеристики квантования, захватываемых сигналов с амплитудой А. \

Вывод (8.74) не приводится, поскольку методика вычисления [А) по существу не отличается1от методики, показанной на примерах типовых нелинейностей в гл. 7.

Соотношение (8.74) записано для б Ц Д = 1. На рис. 8.31 показаны амплитудно-фазовые характеристики U„д (Л) и

нэ (Л). Так как характеристика нелинейного элемента квантования однозначна, то Ц„э (Л) является действительным числом и потому его характеристика совпадает с действительной осью. Максимальное значение 1„э (Л) равно 4/я = 1,27

при а = 12/2 = 0,707. На рис. 8.32 приведена логарифмическая амплитудная характеристика L (а). Последнюю весьма удобно применять для анализ! и синтеза ЦС с непрерывной передачей данных методом ЛЧХ;

Исследование цифровых систем с учетом квантования по уровню и по времени. Цифровые автоматические системы при условии учета квантования как-по времени, так и по уровню следует отнести к классу нелинейных импульсных систем (см. рис. 8.29) и для исследования динамики таких ЦС привлекать соответственно методы, разработанные для нелинейных импульсных систем. Так, для исследования абсолютной устойчивости ЦС используем критерии, разработанный Я-З. Цыпки-ным [81: положение равновесия нелинейной импульсной системы, приведенная непрерывная часп которой устойчива и нелинейная характеристика принадлежит сектору (О, k), будет аб солютно устойчивым, если дл. всех частот в диапазоне (О, зт) выполняется неравенство

1 г + Ке,1Гп„(/ю)>0.

Геометрический смысл да амплитудно-фазовая характ

Рис. 8.31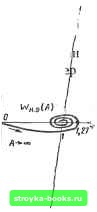

(8.75)

ного неравенства весьма прост: истика WnH (/ю) приведенной линейной части должна располагаться справа от вертикальной прямой - l/k.

Согласно рис. 8.27, характеристика квантования по уровню принадлежит сектору (О, 26/Д), поэтому условие абсолютной устойчивости положения равновесия ЦС выполняется,

если годограф Wnn (/со) располагается справа от вертикальной прямой - Д/(2 б) (рис. 8.33).

В том случае, когда приведенная линейная часть неустойчива, достаточный критерий абсолютной устойчивости (8.75) не выполняется. Это связано с тем, что характеристика