
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [ 38 ] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] § 8.4. Исследование систем с широтно-импульсной модуляцией В § 8.1 было показано, что система с ШИМ является нели-нейной системой, поэтому к ней можно применить известные методы исследования нелинейных систем. Однако при определенных условиях, как было показано в работе [1], систему с ШИМ можно рассматривать как линейную импульсную систему, применив к ней разработанные методы исследования систем с АИМ. Исследование системы с 1Йиротно-импульсной модуляцией по линеаризованной модели., Рассмотрим условия, при которых система с ШИМ эквивалентна системе с АИМ. Для этого, так же как это было сделано в § 8.2 составим основные уравнения системы с ШИМ (рис. 8.37). Определим реакцию линейной части системы на один импульс длительности Ym, о- Здесь Vm, о - относительная переменная длительность импульса на выходе широтно-импульсного модулятора, зависящая от величины сигнала на входе модулятора, т. е. -ут.о = "Vl 11 = "mlT; -х - постоянная величина. Реакция линейной части на такой импульс определяется в момент = т, по аналогии с (8.22), соотношением hy{t-m)=\~" при m<F< m-Ь-у.о; \h(t.m)~h(T- m -у„,„) при m + •Vm,o<<<« ; (8.80) Тогда реакция линейной части системы на последовательность импульсов постошной амплитуды, равной 1, и переменной длительности в моМент t = п на основании принципа суперпозиции будет / вых["1/= S signxlm/ivln-m. , 1 при д:т<0; S!gn;f[ml - Предположи.м, что (8.81) Ц 1 при Aim] >0. Ym.o-=<hl"ll< 1- (8-82) физически условие (8.82) означает, что рассматриваются малые изменения управляющего сигнала или что факти-чесйи длительностью управляющих импульсов (по сравнению с периодом их следования) можно пренебречь. Непрерывная часть Рис. 8.37 Тогда после разложения h (t - т - Ут,о) в ряд по у.о учетом только первой степени у, о реакцию hy {t но записать в виде hy (t-m) = hit-m)-h{t~m-y ym.oh (i-m). m, 0 m) МОЖ- (8.83) Для момента t = n hy{n-т)=ил:[/п]Л(п-tn), тфп. (8.84) • Если n = m, то очевидно, что hy (0) = ft (0). Подставляя соотношение (8.84) в (8.81) и учитывая, что sign х{т\\х{т]\ = х[т\, получаем соотношение, связывающее входную и выходную переменные разомкнутой системы с ШИМ в дискретные моменты времени t = п: лвых [«]=< S х[т\Н[п-т]. (8.85) т= О Сопоставляя (8.85) с (8.24), приходим к выводу, что при условии (8.82) система с ШИМ эквивалентна системе с АИМ коэффициентом усиления и реакцией линейной части hy(i) = h{t). Отсюда следует, что все результаты, полученные в § 8.1 для систем с АИМ, могут быть использованы для систем с ШИМ (если в соотношениях для систем с АИМ принять Уо С 1 и заменить у на oi). Так, выражение для передаточной функции W* (q), аналогичное (8.31), можно представить в виде W*iq) = V Сг (8.86) г= 1 где для систем с ШИМ Выражение для передаточной функции W* (<?), аналогичное (8.36), для систем с ШИМ записывается в виде W*{q)K 2° W{gi-j2nk). (8.87) k= - оо Таким образом, уравнение разомкнутой системы с ШИМ имеет вид Авь,х(9)=И*(<7)*(?) (8.88) и полностью совпадает с уравнением разомкнутой системы в АИМ. Передаточная функция замкнутой системы определяется соотношением (8.34). Для практического исследования систем с ШИМ удобно использовать частотные характеристики разомкнутой системы. Построение частотных характеристик можно выполнить, используя соотношение (8.87), положив в нем предварительно q = /to. Так как выражение для частотной характеристики разомкнутой системы с ШИМ W* (/to) получается значительно более простым по сравнению с выражением (8.37) для систем с АИМ, то и процесс построения W* (/ю) упрощ,ает-ся. На рис. 8.38 иллюстрируется порядок построения W* (/to) для случая, когда частотная характеристика линейной части существенно уменьшается по мере роста частоты со. Упрощенное выражение, аналогичное соотношению (8.38) для системы с АИМ, Рис. 8.3 в этом случае может быть 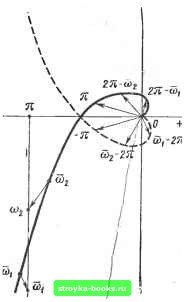 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [ 38 ] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |