получено из (8.87), если в нем ограничиться двумя слагаемыми наименьшей частоты:

U7* (ую) » к ((/ю) -f W [/ (ю - 2я)] 1.

Годограф на рис. 8.38 построе по точкам, соответствующим частотам оз = <0i, сй=<02 со = я. Очевидно, что все методы исследования устойчивости и качества, разработанные в § 8.2 для систем с АИМ, могут быть применимы для линеаризованной системы с ШИМ. Весьма удобным также для реЩения задач анализа и синтеза систем с ШИМ будет и метод логарифмических частотных характеристик, изложенный в § 8.3 применительно к цифровым системам и системам с АИМ.

Исследование периодических колебаний в системах с широтно-импульсной модуляцией. Выше были рассмотрены вопросы исследования систем регулирования с ШИМ-1 по линеаризованной модели, т. е. при небольшой глубине модуляции.

В общем случае система с ШИМ-1 является нелинейной системой и, следовательно, в ней возможны периодические колебания. Здесь мы проведем исследование симметричных периодических колебаний с помощью метода гармонического баланса.

Структурная схема рассматриваемой системы с ШИМ приведена на рис. 8.37. Предположим, что модулируется задний фронт импульса. Тогда импульная последовательность на выходе модулятора может быть определена соотношением

Z т 1 " "Р" nr<t< пТ+у [х (пТ)];

I О при + у [х (пТ)] <:t<:{n Н 1)7

Здесь, как и ранее, б - амплитуда; Т - такт следования импульсов; пи п -f 1 - моменты появления п-го и (п + 1)-го импульсов. Моменты появления импульсов будем называть тактовыми. Если тактовое значгние сигнала на входе модулятора превосходит некоторое пороговое значение 1/х, то соответствующий импульс будет заполнять весь интервал повторения. Такие импульсы будем называть насыш,енными.

. Зависимость у [х {пТ)] = у [х (пТ)]/Т изображена на рис. 8.39. Аналитически она может быть выражена следующим образом:

11 при \х{пТ)1>(1/х).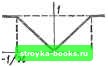

и л(/7г;

Рис. 8.39

Таким образом, при ]х (пТ) \ < длительность импульса пропорциональна модулю входного воздействия, а при больших значениях 1л: {пТ) длительность постоянна и равна интервалу повторения Т.

Если теперь принять во внимание выводы §8.1 и соотношение (8.90), то широтно-импульсную систему (см. рис. 8.38) следует рассматривать как нелинейную, у которой нелинейность обусловлена, во-первых, модуляцией по длительности (квантованием) и, во-вторых, тем, что длительность импульсов является нелинейной функцией входного сигнала (рис. 8.39).

Положим лго = О и предположим, что в рассматриваемой системе установились симметричные, колебания, при которых число положительных импульсов в периоде равно числу отрицательных и что период колебаний равен 2 NT, где N - целое число. Тогда сигнал х {t) будет представлять собой периодическую функцию с периодом, равным 2 NT (рис. 8.40, а).

С выхода модулятора на линейную часть будет в этом случае поступать последовательность импульсов, длительности которых также меняются периодически с тем же периодом 2 NT (рис, 8.40, б). Эти длительности равны „, у, „, yw-i, о и определяются значениями х (0), х (Т),..., х [{N - 1) Т ]

с помош,ью соотношения (8.90). Величины х (0), х(Т),..., x[(N - 1) П являются параметрами периодических колебаний, так как они полностью определяют периодическую последовательность импульсов на выходе модулятора, а следовательно, и выходную величину непрерывной части, которая является реакцией на эту последовательность.

Последовательность импульсов, изображенную на рис. 8.40, б, можно разложить в ряд Фурье, т. е.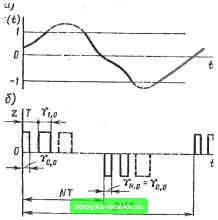

представить в виде суммы гармонических составляющих, причем коэффициенты этого разложения можно выразить через неизвестные параметры х (0), х (Г), xl{N - 1)Т] [11]:

а„ sin {2т - 1) t + cos (2m - 1) t

(8.91)

(2m-l)n b,

N- 1

1 - У cos (2m - I) (I + уо [X (iT)])

£ = 0

(2m - 1) П

ctg(2m-I)

w- 1

- 2 sin(2m-l)-(i-bYo[A:(tT)])

/ = 0

(8.92)

Обозначим частотную характеристику непрерывной части через W (/(о), а величины б и х учтем в приведенной непрерывной части. Тогда частотная характеристика приведенной непрерывной части IFnii (/w) запишется в виде

Г„„ (/©) = 6><Г (/со) = Г„„ (со) еО <-).

(8.93)

Находя по известным правилам и складывая реакции непрерывной части на каждую гармоническую составляющую выражения (8.91), найдем выходную величину непрерывной части:

(2т-1) к

а„ sm

+ bm cos

(2m-l)-i H-ef-ILZ±„] ЛТ \ NT I

(8.94)

Если в системе установились периодические колебания, то Л значений переменной х„ых (О в тактовые моменты времени t -О Т, 2Т, {N - I) Т должны быть равны N значениям сигнала