
 |
|
Главная Нелинейные системы управления [0] [1] [2] [ 3 ] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] Для изучения характера траекторий часто удобно упростить выражения, рассмотрев начало движения от одной из осей. Так, если f/o = 0, то X = Хо cos Шо /; у=: -(Ло sin «о t, (7.7) Начало координат в рассмотренном примере представляет собой особую точку, не принадлежащую ни одной из траекторий и называемую точкой типа центра. Эта точка устойчива lio Ляпунову. Действительно, если задано положительное, сколь угодно малое число е, то мы всегда можем выбрать эллипс, у которого большая полуось была бы меньше е, т. е. max (С/юо, С) <: е, и далее выбрать Хц и Уо так, чтобы было уЬ + -fcjoX <Г С. Тогда X (t) и у (t) по модулю не превзрйдут е при любом t. Однако с практической точки зрения движение консервативной системы трудно назвать устойчивым, поскольку при наличии случайных помех возможно принципиально неограниченное «блуждание» амплитуды колебаний. Консервативную систему считают находящейся на границе устойчивости. Это пример редкого исключения, когда определение устойчивости по Ляпунову вступает в противоречие с представлением об устойчивости на основе «здравого смысла». Система с сухим кулоновским трением. Пусть теперь в рассмотренной системе действует постоянная по значению сила трения /.jp, направленная навстречу движению. Для удобства выразим эту силу в виде произведения cog на некоторое положительное число е, т. е. . . . / тр coge, х<0; -С0о8, х>0. (7.8) Когда система движется, динамическая сила, создающая ускорение X, и сила пружины cogx уравновешиваются силой тре-ния: х + о)§х=/.,р, хфО. Этр имеет место, когда соох>/5.р или х > е. Тогда избыток силы юох - расходуется на создание ускорения. Если же усилие, развиваемое пружиной, меньше силы трения, то система не сможет сдвинуться с места: ; x + fi)§x = G; :(х;е,. х = 0. Таким образом, движение на разных стадиях описывается различными дифференциальными уравнениями: -шое, л:>0, л: >8; О, х=0, \ х\е; (7-9) cog8, л:<0. х>е. Уравнение с верхней правой частью определяет фазовую траекторию в верхней полуплоскости, с нижней правой частью - в нижней полуплоскости, средняя правая часть соответствует отрезку покоя на действительной оси - е < л:<е. Этот отрезок является геометрическим местом бесчисленного множества возможных точек равновесия. В верхней полуплоскости движение определяется уравнением x + wg(x + 8) =(x + 8)"+tug(x-f 8) = 0, л:>0. Сопоставляя с (7.3), видим, что это эллипс, центр которого смещен в точку - е на оси х. Соответственно в нижней полуплоскости л;-f cog (л: - 8) = (х -8)" -Ь (og (х-- е)=0, х < О, имеем семейство эллипсов с центром в точке + 8 на оси х (рис. 7.9, а). Смещение эллипсов приводит к тому, что изображающая точка, пересекая ось х, переходит на эллипс меньшего размера и в конце концов приходит на отрезок покоя. Так как к любой точке отрезка покоя фазовые траектории подходят сверху и снизу, изображающая точка, попав на отрезок покоя, остается на нем; следовательно, отрезок покоя устойчив. Ось абсцисс точками - 8, 8 делится на три части: внутреннюю - отрезок покоя и две внешних 1х > е, на которых при переходе из одной полуплоскости в другую происходит изме нение уравнения движения. Таким образом, ось абсцисс за пределами отрезка покоя является линией перехода с одного закона движения на другой. Такие линии называют линиями переключения. Уравнения движения, получаемые в результате решения дифференциальных уравнений (7.9), при начальных условиях X = Хоуу = Уо = о имеют вид: 1-й полуэллипс в нижней полуплоскости л; = е + Хо COS ojo. О < / < я/шо = А; 1-й полуэллипс в верхней полуплоскости X = - е + (Хо - е) cos wj, fi< t<: 2t\ 2-й полуэллипс в нижней полуплоскости X = е + (Хо - 2е) cos vtj... и т. д. Амплитуды последовательных колебаний убывают по линейному закону (рис. 7.9, б), что качественно отличает характер затухания колебаний в нелинейной системе с сухим трением от экспоненциального затухания в линейной системе. Время затухания в линейной системе бесконечно, в рассматриваемой нелинейной - конечно. В коротких и жестких пружинах возникает сила внутреннего трения от смещения сечений во время изгиба пружины. Внутренние напряжения перпендикулярны смещающимся сечениям и пропорциональны деформациям. Сделав допущение, ЧТО! силы внутреннего трения, подобно силам сухого кулонов- 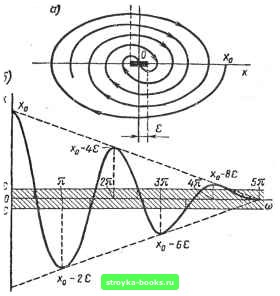 Рис. 7.9 [0] [1] [2] [ 3 ] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |