
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [ 42 ] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] (8.109) Импульсная последовательность на выходе модулятора согласно (8.13) определяется соотношением 6sinA;(i„) при 2„<i„ + Y; О при i„ + Y<<W где /„+1 - моменты появления п-го и (п + 1)-го импульсов; 7, б - длительность и амплитуда импульсов соответственно. Дифференциальное уравнение, связывающее вход НЭ и вход линейной части и описывающее движение системы с линейной частью (8.108), запишем в виде Toy+y=-koZ, (8.110) где г определяется соотношением (8.109). Так как на линейную часть, согласно (8.109), действует импульсный сигнал, принимающий значения + 6, - б, О, то фазовая плоскость заполняется тремя семействами кривых, уравнения которых легко получаются из (8.110) с учетом (8.109): у = -- ТдХ + Су при z = 0; (8.111а) = То [kz In \х + koZ\~ х] + Сг при гфО. (8 1116) Вид кривых показан на рис. 8.44. Кривые на рис. 8.44, с соответствуют сигналу z отрицательной полярности (z = - - б), кривые на рис. 8.44, б - положительной (z = + б), а прямые на рис. 8.44, в соответствуют паузе между импульсами (Z = 0). Для построения траектории движения по полученным фа зовым траекториям необходимо определять моменты переклю- в) . 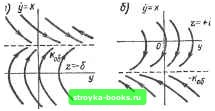 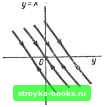 чения с траекторий импульса (8.1116) на траектории паузы (8 111а) и наоборот. Отметим, что определение точек переключения в конце каждого периода, т. е. в моменты ti, t-.-., tn, трудностей не вызывает, поскольку моментам t, g,..., t соответствует изменение координаты у от момента t на величину Д, 2Д, пД (в соответствии с уравнением (8.13)). Для определения координат точек переключения в моменты окончания импульсов, т. е. в моменты + у, t \у..... 4: у„ найдем приращение координаты у за время п-го импульса А t/n- Обратимся к уравнению (8.110). Его решение имеет вид / = /о-;б(<-дч-Т(А:обН-Хо)(1-е<--»)/а (8.112) где Хо, Уо - значения х, у в момент t == Отсюда, полагая, что в качестве tg взят произвольный момент времени tn, получаем А«/п = У (tn + У)-У (tn) ==b-i сх (tn), (8.113) 6= ~kob{y-To{\ -e-v/r.j)-const; с = Го(1 -e-v/7-„) const. Таким образом, из соотношения (8.113) следует, что приращение координаты У за время п-го импульса у линейно зависит от значения х (tn) в момент появления п-го импульса. Как показано на рис. 8.45, зависимость (8.113) удобно отобразить на фазовой плоскости. По ней для значения х („) определяется величина Аг/„. Проводя вертикальную прямую, отстоящую от прямой пД на величину Д£/„, находим точку пересечения ее с фазовой траекторией импульса, проходящей через точку (х (tn), п&). Точка пересечения соответствует окончанию п-го импульса, т. е. моменту tn + у. Далее процесс построения проводится аналогичным образом. На рис. 8.46 построена траектория движения, соответствующая затухающему процессу. Здесь на участке to - i, т.е. до момента появления первого импульса, движение происходит по траектории паузы (8.111а). В момент t появляется импульс положительной полярности г = + б, так как х (4) > 0; точка, соответствующая моменту t + у, определяется по изложенному выше правилу. Движения на участке паузы t + + Y - 2 происходит по траектории (8.111а). Изменение координаты у за один период у (t) - у (ti) == Д. За время паузы та I {п-1)й Рис. 8.45 У-Х. Рис. 8.46 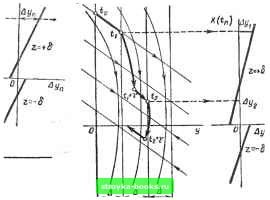 УИ,) У(*,] y(h во втором периоде, т. е. при > + Y фазовая траектория приходит к отрезку равновесия. В случае, показанном на рис. 8.47, по окончании п-го периода в момент /„.1 возникает импульс отрицательной полярности, поскольку у (tn+i) - у (О -Д. Определяя последовательно координаты точек в моменты „ + у, tn+i, n+i+ +Y» 4+2> несложно показать, что в этом случае образуется замкнутый цикл л; („+2) = х [tn), соответствующий в реальной системе режиму периодических колебаний, представляющих собой чередование разнополярных импульсов (рис. 8.48); число импульсов за период колебания N = 2. 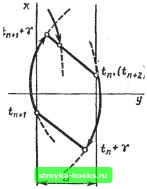 S о -S ТТ тт nzznr Рис. 8.47 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [ 42 ] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |