Частотно - импульсный модулятор

"ШТ

«оси

Рис. 8.49

Соотношение параметров системы с ИЧИМ, при котором возможны периодические колебания (оно приводится без доказательства), имеет вид

кфу > Д. (8.114)

Пользуясь соотношением (8.114), можно выбрать параметры модулятора (б, Y, Д) или коэффициент передачи kg объекта управления, чтобы устранить периодические колебания в рассматриваемой системе с ИЧИМ.

Исследование устойчивости в целом частотно-импульсных систем 2-го рода. Для исследования устойчивости в целом системы с ЧИМ 2-го рода удобнее воспользоваться структурной схемой, предложенной Я.З. Цыпкиным в работе [10]. Здесь эквивалентная ЧМ-модулятору схема представлена в виде релейной следящей системы, работающей в скользящем режиме (рис. 8.49). Линейный фильтр К (s) в случае ИЧИМ имеет передаточную функцию К (s) = kls, РЭ - релейный элемент, характеристика которого показана на рис. 8.50;

/Coc(s) = и/г, где г= lim sK (s) - k.

(8.115)

Если в качестве фильтра К (s) использовать не интегратор, а апериодическое звено с передаточной функцией К (s) = kl (1 + sT,) и соответственно в качестве звена обратной связи - элемент с передаточной функцией Кос (*) = *о/. где, согласно (8.115), г =s к, /Tl, то получим так называемую сигма-ЧИМ (2-ЧИМ).

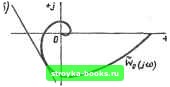
Рис. 8.90

Рис. 8.51

В соответствеии с предложенной структурной схемой частотно-импульсная система может рассматриваться как релейная система с внутренней обратной связью, предназначенной для создания скользящего режима (рис. 8.51). Здесь передаточная функция общей линейной части Wq (s) имеет вид:

Wo(s) =: IW(s) + VH /C(s),

(8.116)

где W (s) - передаточная функция линейной части в частотно-импульсной системе.

Таким образом, исследование частотно-импульсной системы (с ИЧИМ или Е-ЧИМ) сводится к исследованию релейной системы. В этом случае, используя известный критерий устойчивости релейных систем, можно сформулировать следующий критерий устойчивости частотно-импульсной системы [101: для того чтобы система с ЧИМ была устойчива в целом, достаточно, чтобы общая линейная часть эквивалентной релейной системы была устойчива или нейтральна, а частотная характеристика общей линейной части удовлетворяла условию

Re (1 -Ь (5/и) U/o (М -- > 0.

(8.117)

Используем понятие модифицированной частотной характеристики Wf, (/о), где

i/o(to) = (;o(o3)=RelFo(/to); Vo (w) =toVo (to) = CO Jm Wo (M-

(8.118)

Тогда критерий устойчивости в целом можно сформулировать так: частотно-импульсная система управления будет устойчива в целом, если модифицированная частотная характеристика общей линейной части эквивалентной релейной системы ле-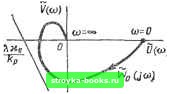

Рис. 8.52

жит справа от прямой Попова, проходящей через точки -Ык и имеющей неположительный наклон (рис. 8.52).

Так как частотная характеристика общей линейной части получается из (8.116) при подстановке S = ju), т. е.

1Го(/о>) = [W(/«)-f>Co/rl/С(/о>),

то характеристику Wo (/w) можно построить следующим образом (рис. 8.53):

1. Построим частотную характеристику линейной части W (/со) = и. (о) + jV (©) (кривая / на рис. 8.53, а).

2. Сместим ее вправо на величину к/г (кривая 2) и перемножим с частотной характеристикой К (/to) (для Е-ЧИМ кривая .5).

3. Таким образом найдена Wo (/о). Изменяя каждую ординату ее в to раз, получаем Wo (/©) (рис. 8.53, б). Проводя прямую Попова с неположительным наклоном, определяем конкретные параметры, при которых частотно-импульсная система устойчива в целом.

Для ИЧИМ, где

получаем

Wo(/o) = (ir(/£o) + >co/rl-,

Uo (о) - 1/ («))Jm W (/о>);

(8.119)

Vo (w) == - [ (/ (Ц + Ко/г] kr--liiV (to) - По-

(8.120)

Таким образом, для ИЧИМ Wo (/») можно построить непосредственно по действительной и мнимой частям W (/о).