
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [ 44 ] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166]  rj Исследование периодических режи- мов в системах с ИЧИМ. В системах с ИЧИМ, как и D других нелинейных системах, прн невыполнении условий устойчивости в целом возможно возник-новепие периодических колебаний. Колебания ранга N=2 мы уже наблюдали прн исследовании системы с ИЧИМ и простейшим объектом управления первого порядка, когда изучали метод фазовой плоскости. Рис. 8.54 Исследование периодических колеба- нии в система.х с ИЧИ.М произвольного порядка удобно провести, пользуясь методом гармонического баланса. Обратимся к структурной схеме, приведенной на рис. 8.43, и преобразуем ее к виду рис. 8.54. Преобразованная схема состоит из известного нелинейного элемента квантования приращений и приведенной непрерывной части с передаточной функцией lF„„(s)=\l/(s)(l-e-v)/s. Условие существования периодических колебаний в такой системе, согласно методу гармонического баланса, запишем в виде И?.,эИ)1..„(усо)= -1. (8.121) где VV-iig (Л) - эквивалентный комплексный коэффициент усиления НЭ квантования приращений. Особенности НЭ квантования приращений (и, в частности, его отличие от характеристики квантования по уровню) рассмотрены в § 8.1. Учтем эти особенности прн выводе комплексного коэффициента усиления. Если приведенная непрерывная часть является фильтром низких частот, то пернодическш про цесс на входе НЭ имеет вид гармонического сигнала: у (/) = = А sin со, где И, о- амплитуда, частота гармонического сигнала. В зависимости от амплитуды А в периодическом процессе будет участвовать различное число ступеней квантования и со-ответствеино на выходе модулятора будут иметь место колебания различного ранга N, т. е. колебания с различным числом N импульсов в периоде. Для различных типов колебаний многоступенчатая характеристика квантоваппя приращений (аналогично тому, как это делалось для характеристики квантования но уровню, см. § 8.3) может быть заменена либо тнг.овой релейион характеристикой, либо комбинацией типовых характеристик так. как показано па рнс. 8.55, а -г .чля Л = 2, 4, 6, 8. При таком представлении пелниенпого элемента квантования приращений его эквивалентный комплексный коэффициент усиления выражается сум.>,(он аналогичных коэффициентов усиления типовых релейных элементов. Необходимо только подчеркнуть, что типовые релейные элементы, из которых со-
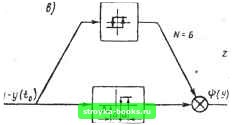 •/•yd,) 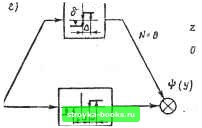 п п п п...... IJ UUUt ставляется схема замещения НЭ. квантования приращений, принципиально отличается от обычных релейных элементов, которые рассматривались, например, в гл. 7. Это отличие состоит в том, что, согласно уравнениям ИЧИ-модуляции (8.12), (8.13), моменты переключения определяются не абсолютным значением входного сигнала, а величиной разности сигнала y{t) и его значения у (to) в момент to начала преобразования. Поскольку периодический режим представляет собой (рис. 8.55) чередование групп положительных и отрицательных импульсов, можно условно за принять момент появления пос-следнего отрицательного импульса предьщущей группы. Рассмотрим вывод эквивалентного комплексного коэффициента усиления на примере N = 2 (рис. 8.55, а): ..z{A)g(A) + Jh(A), (8.122) где 2 Щ = (cos (pi - cos Фа); (Л) = (sin - - sin фх); фх = 0), ф2 = 0)2 - значения аргумента периодического сигнала у (t), при которых происходит скачкообразное изменение сигнала я]? (у); соответственно t, t, - моменты появления импульсов на выходе модулятора. Выражение для определения и фг запишем в виде У (к) - У (д=Д, У (У = У (Q. (8.123) а с учетом гармонического характера сигнала у (t) из соотношений (8.123) получаем Ф1 = arcsin sin Ф + ); Фг = Ф. (8.124) где Ф - значение аргумента у (t) в момент начала преобразования, т. е. у (to) = А sin Ф. Соотношения (8.122), (8.124) полностью определяют значение 1нэ, 2 (А) эквивалентного комплексного коэффициента усиления нелинейного элемента квантования приращений для режима колебаний ранга N - 2. Аналогичные соотношения несложно получить для N = 4, 6, 8 ИТ. д. На рис. 8.56 для удобства графического решения уравнения периодического режима (8.121) построены нормированные обратные амплитудные характеристики .V (Л)]-» для iV = 2, 4. 6, 8 и различных Ф: [ WI. N (Л)]-» = [ Г„3. N (А)] 6/Д. (8.125) [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [ 44 ] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |