
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [ 45 ] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] Р.--1 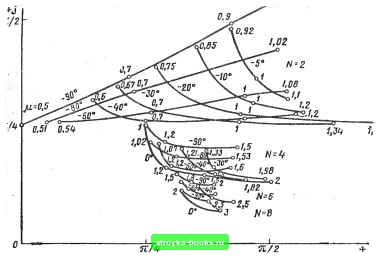 Рис. 8.56 Как видим, эти характеристики занимают ограниченные области комплексной плоскости, каждая из которых соответствует одному определенному N. При этом каждая область объединяет семейство характеристик, соответствующих различным значениям Ф при одном и том же N. Особенностью полученных характеристик, помимо зависимости их от фазы Ф, является то, что эти характеристики, соответствующие определенным и Ф, имеют место лишь в определенной области значений амплитуды А (или относительной амплитуды р = А /Д), как показано на рис. 8.56. Построив в одних осях характеристику [Whs.n {А)]- и годограф - IFiiH (/to)., по точкам пересечения определяем наличие и параметры периодического режима. Если годограф ~ пн (/to) пересечет несколько областей [ W„3. лг(Л)]-, соответствующих различным /V, то это означает, что в системе с ИЧИМ при данных параметрах возможны периодические режимы различных рангов (в зависимости от различных началь-нь1х условий). На рис. 8.57 для примера проведено графическое исследование колебаний в системе с ИЧИМ, имеющей следующие па- 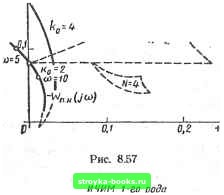 \ н.э. <2)f 1 t W(S) Рис. 8.58 раметры: W (s)) = 0(1 + sTX = 2; To = 0,5 c; у =0,1 с; б/Д = 10. 2(e-o-i /« -1) Годограф - 1Гпн {/«) = в этом случае ка- пн ут(1+/ш . 0,5) сается области {1„э, 2 ()Ь. Если коэффициенты Jfeo уве- личить, например до 4(е-0.1/« > = /а.(1+0,5/ш) будет feo = 4, то годограф - 1Г„„ (/(о) = пересекать область [lF„.j,2 (Л)]"*, что говорит о наличии колебаний N = 2 с параметрами А » 0,6 Д; to « 12 с- Исследование периодических колебаний в системах с ИЧИМ 1-го рода. Используя структурные схемы ИЧИМ 2-го рода (см. рис. 8.7) и общую структурную схему модулятора 1-го рода (см. рис. 8.10), можно построить структурную схему системы управления с ИЧИМ 1-го рода в виде, показанном иа рис. 8.58. Такая система является нелинейной импульсной системой, однако если учесть, что последовательное соединение фиксатора нулевого порядка и интегратора представляет собой достаточно хороший фильтр, то, согласно выводам § 8.2, импульсную часть можно рассматривать как непрерывную с передаточной функцией f О ~ e-)/s, и, следовательно, система с ИЧИМ 1-ро рода может рассматриваться как нелинейная система с нелинейным элементом квантования приращений и приведенной непрерывной частью W],„ (/«) - W (S) (1 -е-»0 (1 - е- v)/(Ts). Очевидно, что в этом случае для исследования периодических колебаний можно использовать результаты предудущего параграфа, в первую очередь характеристики Ш„э. N {А)]-. Решение уравнения периодического режима в системе с ИЧИМ 1-го рода \ + W„.n(A). W„(/to)=.0 можно выполнить графически, определив точки пересечения характеристик [„э. n (А)]- с годографом =- wl,, (/to). [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [ 45 ] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0014 |