
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [ 47 ] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] Для любого фиксированного момента времени, например ( = реализация случайного процесса Xj (t) представляет собой конкретную величину, значение же случайной функции X (ti) является случайной величиной, называемой сечением случайного процесса в момент времени t. Поэтому нельзя утверждать, что случайный процесс в данный момент времени имеет такое-то детерминированное значение, можно говорить лишь о вероятности того, что в данный момент времени значение случайного процесса как случайной величины будет находиться в определенных пределах. Статистические методы изучают не каждую из реализаций Xi (t), образующих множество X (t), а свойства всего множества в целом с помощью усреднения свойств входящих в него ре- 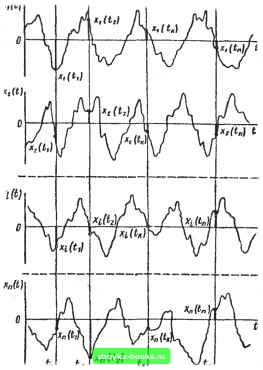 ализаций. Поэтому при исследовании автоматической системы управления судят о ее поведении не по отношению к какому-либо определенному воздействию, представляющему заданную функцию времени, а по отношению к.целой совокупности воздействий. Как известно, статистические свойства случайной величины X определяют по ее функции распределения (интегральному закону распределения) F (х) или плотности вероятности (дифференциальному закону распределения) w {х). Случайные величины могут иметь различные законы распределения: равномерный, нормальный, экспоненциальный и др. Во многих задачах автоматического управления очень часто приходится иметь дело с нормальным законом распределения (или законом Гаусса), который получается, если случайная величина определяется суммарным эффектом от действия большого числа различных независимых факторов. Напомним, что случайная величина х при нормальном законе распределения полностью определяется математическим ожиданием (средним значением) тх и средним квадратическим отклонением а. Аналитическое выражение функции распределения в этом случае f e-(-"-)/<">d.v. (9.1) У2л Од, J - ОО Следует обратить внимание на то, что, хотя в (9.1) переменная интегрирования и верхний предел интегрирования обозначены одним символом, это не отражается на конечных результатах и не должно привести к недоразумениям. Аналитическое выражение плотности вероятности для нормального закона распределения 2 е-(-"=)/("-). (9.2) dx У2л Типичные графики функций распределения F (х) и плотности вероятности w (х) для различных значений приведены на рис. 9.2, а, б. Изменение среднего значения т вызывает только смещение кривых F (х) и w{x) вдоль оси абсцисс без изменения их формы, а изменение величины Сх вызывает изменение масштаба вдоль обеих координатных осей, причем площадь, ограничиваемая кривой w (х) и осью абсцисс, всегда остается конечной и равной единице, т. е. J w{x)dx=F{x) J =1, (9.3) -- ОО - оо поскольку F (оо) = 1, а F (-оо) ~ 0. 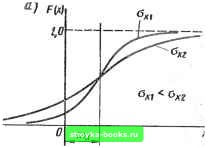 При конечных пределах интегрирования величина интеграла, определяемого (9.3), будет меньше единицы. Однако уже при пределах интегрирования от (Шх - до (т + 4- ЗОх) величина интеграла равна 0,997. Так как вероятность того, что X лежит между (тх - Зос) и (т + За,,), равна 0,997, то величину За часто используют в практических расчетах в качестве верхней границы отклонения от среднего значения. Для случайного процесса также вводят понятие функции распределения F {х, t) и плотности вероятности W (х, f), которые зависят от фиксированного момента времени наблюдения г? и от некоторого выбранного уровня X, т. е. являются функциями двух переменных: xut. Рассмотрим случайную величину X {tl). т. е. сечение случайного процесса в момент времени ti. Одномерной функцией распределения (функцией распределения первого порядка) случайного процесса X {t) называют вероятность того, что текущее значение случайного процесса X (ti) в момент времени 4 "с превышает некоторого заданного уровня (числа) т. е. 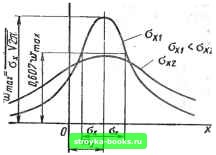 Рис. 9.2 Fl (Xi, tl) = Р {X (tl) < Xi}. (9.4) Если функция Fl (Xi, ti) имеет частную производную по Xi, т. е. wi (Xi, tl) = dFi (Xi, tiVdXi, (9.5) TO функцию Wi (Xi, i) называют одномерной плотностью вероятности (плотностью вероятности первого порядка) случайного процесса. Величина Wi (xi, tl) dxi P{xi < X (tl) < Xi -b dxi) (9.6) [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [ 47 ] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0016 |