Математическое ожидание случайного процесса X (t) представляет собой некоторую неслучайную (регулярную) функцию времени (t), около конторой группируются и относительно которой колеблются все реализации данного случайного процесса (рис. 9.3).

Математическое ожидание случайного процесса в каждый фиксированный момент времени 1к равно математическому ожиданию соответствующего сечения случайного процесса X (t) и -представляет собой операцию вероятностного усреднения случайной величины X (ty), при котором каждое возможное значение для случайной величины х принимается с весом, равным элементу вероятности (х , t dx [см. (9.6)]. Математическое ожидание называют средним значением случайного процесса по множеству (средним по ансамблю, статистическим средним), поскольку оно представляет собой вероятностно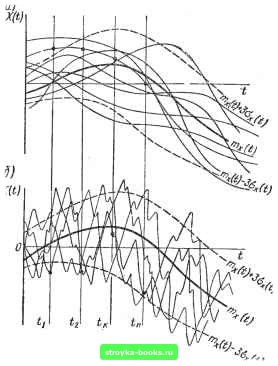

усредненное значение бесконечного множества реализации случайного процесса.

Средним значением квадрата случайного процесса называют величину

?(0 -Л/1{Х(0}1 = j xw,{x,t)dx. (9.16)

- оо

Часто вводят в рассмотрение так называемый центрированный случайный процесс X (i), под которым 1юнимают отклонение случайного процесса X {t) от его среднего значения

(i), нлн

X (О = Л (О-ШЛО- (9.17)

Тогда случайный процесс X (/) можно рассматривать как сумму двух составляющих: регулярной составляющей, равной ма-те.матическому ожиданию (t), н центрированной случайной составляющей X (t), т. е.

X (ОЛО + (О- (9.18)

Очевидно, что математическое ожидание центрированного случайного процесса равно нулю:

М [X (01 = /И [X (О -т, (01 (О- (О = 0.

Для того чтобы каким-то образом учесть степень разбросанности реализации случайного процесса относительно его среднего значения, вводят понятие дисперсии случайного процесса, которая равна математическому ожиданию квадрата центрированного случайного процесса:

СЛ0=ЛП(Х(0)=1 = ] {x-mAt)VwAx, t)dx. (9.19)

- со

Дисперсия случайного процесса является неслучайной (регулярной) функцией времени (0. значение которой в каждый момент времени /„ равно дисперсии соответствующего сечения X (/ft) случайного процесса.

Легко показать, что математическое ожидание (f), дисперсия (t) н среднее значение квадрата {t) случайного процесса, имеющие размерность квадрата случайной величины, связаны соотношением

?(t)=D,{i) + mlit). (9.20)

Из (9.20) Еидпо, что среднее значение квадрата случайного процесса (О " определенной мере учитывает и среднее значение случайного процесса, и степень рассеяния его реализаций относительно этого среднего значения, поэтому оно широко используется в качестве оценки точности систем автоматического управления.

На практике часто бывает удобно пользоваться статистическими характеристиками случайного процесса, имеющими ту же размерность, что и сама случайная величина. К таким характеристикам относят:

среднее квадратическое значение случайного процесса

с.„ (t) = = Vd7W+M (9.21)

равное арифметическому значению квадратного Kopirn из среднего значения квадрата случайного процесса;

среднее квадратическое отклонение случайного процесса

oAt)VDAt), (9.22)

равное арифметическому значению квадратного корня из Дисперсии случайного процесса.

Из (9.21) и (9.22) видно, что среднее квздратическое значение Хек (О и среднее квадратическое отклонение (t) случайного процесса в общем случае не совпадают. Последняя характеристика используется только для центрированных случайных процессов.

В заключение заметим, что хотя ни мате.матнчсскос ожидание, ни дисперсия случайного процесса ни в какой мере не характеризуют степень статистической зависимости между сечениями случайного процесса в различные моменты времени, знания этих характеристик часто достаточно для решения многих задач теории автоматического управления.

§ 9.3. Корреляционные функции случайных процессов

Математическое ожидание и дисперсия являются важными характеристиками случайного процесса, но они не дают достаточного представления о том, какой характер будут иметь отдельные реалпзанип случайного процесса. Это хоропю видно "3 рис. 9.3, где показаны реализации двух случайных процес-*ов, совершенно различных по своей структуре, хотя и имею-