
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [ 4 ] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 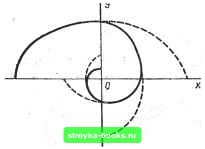 Рис. 7.10 Рис. 7.11 ского трения, пропорциональны нормальным давлениям, а по направлению - противоположны скоростям движения, получаем следующую систему уравнений: (7.10) л: + (wo -Ь k) л: = О, sign х - sign х\ X + (cog -k) л: = О, sign х - -sign х. В первом и третьем квадрантах фазовой плоскости знаки жил: совпадают и фазовыми траекториями будут отрезки концентрических эллипсов с отношением вертикальной полуоси к горизонтальной, равным Ыа = Vcoo + k- Во втором и четвертом квадрантах это отношение равно Vcoo - Фазовые траектории скручиваются к началу координат (рис. 7.10). Для малых движение будет близким к движению линейной системы по уравнению X + 2/1э X -f Шэ л; = О, демпфирование; fe/(cL)oJx) - эквивалентное = (Во - частота колебаний. Система с отрицательной восстанавливающей силой. Для получения быстрых перебросов механических деталей из одного положения в другое использукэт пружины, стремящиеся увеличить возникающее отклонение (рис. 7.11). При малых отклонениях от вертикальной линии (состояния равновесия) уравнение системы будет . х - 0)0 л; = р. Уравнение фйзовой траектории dyldx = ыЬх/у. Интегрируя, получаем (aoxdx-ydy=0; (7.12) Рис. 7.12 Это уравнение гиперболы (рис.. 7.12). Начало координат представляет собой особ/ю точку типа седла, соответствующую неустойчивому состоянию равновесия. Если упругая сила является нелинейной функцией, т. е. 0)0 = ф (х), и при значении л; = лга обращается в нуль и меняет знак, то на оси х фазовой плоскости возникают две особые точки: X =0 (центр) и л: = л:„ (седло). Фазовый портрет системы показан на рис. 7.13. Траектория, проходящая через седло-вую точку и показанная на рисунке жирной линией, делит фазовую плоскость на три области с различным характером движения: область / с замкнутыми траекториями и равновесием типа центра и области а и 116 с траекториями, уходящими в бесконечность, и седловой особой точкой. Такие траектории, разграничивающие области качественно различных движений, называют сепаратриссами. Линейная колебательная система с вязким трением. При наличии силы сопротивления движению, пропорциональной скорости (так называемой силы вязкого трения), уравнение системы будет..... x + 2/ix-f ох-О; Л>0. V 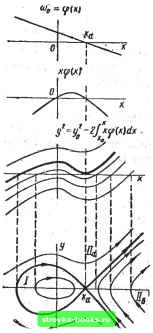 При этом корни характеристического уравнения При комплексных корнях, когда <С соо, имеем Si 2= -h±ja, cl) = Vcl)o - h. Решая уравнения (7.13) при начальных условиях х (0) = х. у (0) = г/о. получим X •= [{уо + /iXo)/cu] е - sin ыг + лго е -cos сог. (7.14) Для исследования характера траекторий поместим точку Хо, г/о на ось абсцисс. Тогда х (0) = Хо, г/ (0) = О и X = Хо е~(Л sin (о/ы + cos ш); г/= - Xoe-(/i/(u + cl))sincuf. (7.15) Кривые X {t) и у (f) представлены на рис. 7.14. Нетрудно видеть, что каждое из последующих пересечений фазовых траекторий с осью х будет ближе к началу координат, чем предыдущее. Траектории представляют собой скручивающиеся к началу координат спирали (рис. 7.15, а). Начало координат является особой точкой типа фокуса: любая траектория с течением времени приближается к ней сколь угодно близко, но угол вхождения траектории в фокус установить невозможно, поскольку dyldx в точке х = г/ = О не существует. При отрицательном демпфировании h -< О фокус неустойчив и траектории будут от него беспредельно удаляться. Движение представляет собой колебания с нарастающей амплиту-Рис. 7.15 дой (рис. 7.15. б). 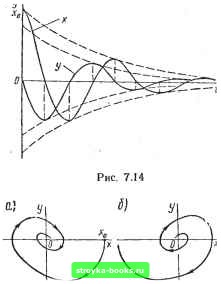 [0] [1] [2] [3] [ 4 ] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |