
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [ 52 ] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] ного применения к регулярной функции x{t) операции, выражаемой интегралом: RAx)x(t)x(t + x)Vim-j j x{t)x{t + T)dL Приведем некоторые основные свойства корреляционных функций /?а:(х). 1. Начальное значение корреляционной функции 1см. (9.33)] равно дисперсии случайного процесса: RAO)D,, (9.38) 2. Значение корреляционной функции при любом т не может превышать ее начального значения, т. е. RAO)>\RA-)l (9.39) Чтобы доказать это, рассмотрим очевидное неравенство lx(t) ± ± x(t + т)]" > 0. из которого следует xV) + xV + "t) > > 2x{i)x{t + т). Находим средние значения по времени от обеих частей последнего неравенства: х (О + хЦ1 + х)= х* (О + x(t+x) = х (О + х (О = 2х = 2D, = 2R (0) и 2х (t) X (t -\- х) -= 2/? (т). Таким образом, получим неравенство RiO) > 1/?1:(т). 3. Корреляционная функция есть четная функция т, т. е. RAx)-RA-r). (9.40) Это вытекает из самого определения корреляционной функции. Действительно, Rx W -[х (О-х\ [X (/ -f т) -х1 = = [х (/-т)-х]1х(0-х] » R, (-т). поэтому на графике корреляционная функция всегда симметрична относительно оси ординат. 4. Корреляционная функция суммы случайных процессов Z(0 = ХЦ) + C{t) определяется выражением Rr (т) = Rx (т) + Rg (т) + R,s (т) -Ь Rsx (т). (9.41) где Rxgi) и Rgxix) - взаимные корреляционные функции Действительно. Rr iV - М [{X(О + G {/)} {X it +т) G {t + t)}1 -= = M[X (OX(/ + t)] + M[G(OG(f+ t)] + M[X(OG( + t)] + + M [G (0 X -f t)] = (t) + (t) +. (t) + R,, (t). 5. Корреляционная функция постоянной величины x(t) = r= v4o равна квадрату этой постоянной величины Al (рис. 9.5, о), что вытекает из самого определения корреляционной функции: RAV-x (/) x(l + r) =ЛЛ = АЬ. (9.42) 6. Корреляционная функция периодической функции, например x(t) = Л51п(о)1 i + ф), представляет собой косинусоиду (рис. 9-5, д), т. е. /?,;(т) =(Л72)со5а)1т, (9.43) имеющую ту же частоту ы, что и x{t), и не зависящую от сдвига фазы ф. Чтобы доказать это, заметим, что при нахояедении корреляционных функций периодических функций x{t) можно использовать следующее равенство: т т, JC (О JC (М-т) = - f xit)x(t + T;)dt, lim - где Го = 2л/о>о - период функции л;(/). Последнее равенство получается после замены интеграла с пределами от -Т до Т при Т оо суммой отдельных интегралов с пределами от (fe - \)То до кТ, где Л = О, ±1. ±2, .... ±п, и использования периодичности подынтегральных функций. Тогда, учитывая сказанное выше, получим г. R (т) = -1- Г А sin (й, / + ф) sin [wj (/ + т) + <pl dt - г J- Г [cos toi т - cos (wi T + / + 2ф)1 dt: 0 J .: = (i4*/2)coscc»iT, 7. Корреляционная функция временной функции, разлагаемой в ряд Фурье: ft= 1
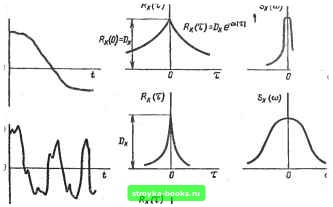 Se.ib/u ш1/М  RxiV-NSiZ)
с Ы at Кл/. w [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [ 52 ] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0012 |
|||||||||||||||||||||