
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [ 56 ] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] Спектральной функции, определяемой по (9.65), соответствует корреляционная функция i?,(T)=- Г -e/--dco=D,e которая полностью совпадает с корреляционной функцией, определяемой по (9.45). Из рис. 9.5, б,в видно, что чем шире график спектральной плотности Sx (ш), тем же график соответствующей корреляционной функции Rx (т), и наоборот, Это соответствует физической сущности процесса: чем шире график спектральной плотности, т. е. чем более высокие частоты представлены в спектральной плотности, тем выше степень изменчивости случайного процесса и тем же графики корреляционной функции. Другими словами, связь между видом спектральной плотности и видом функции времени получается обратной по сравнению со связью между корреляционной функцией и видом функции времени. Это особенно ярко проявляется при рассмотрении постоянного сигнала и белого шума. В первом случае корреляционная функция имеет вид горизонтальной прямой, а спектральная плотность имеет вид б-функции (см. рис. 9.5, а). Во втором случае (см. рис. 9.5, г) имеет место обратная картина. 6. Спектральная плотность случайного процесса, на которой наложены периодические составляющие, содержит непрерывную часть и отдельные 6-функции, соответствующие частотам периодических составляющих. Отдельные пики на графике спектральной плотности указывают на то, что случайный процесс смешан со скрытыми периодическими состав- 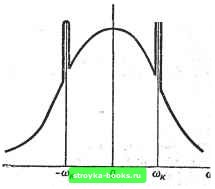 ляющими, которые могут и не обнаруживаться при первом взгляде на отдельные , записи процесса. Если, например, на случайный процесс наложен один ие-. риодический. сигнал ...Ci частотой са, то график; спектральной плотности имеет вид, показанный на рис. 9.10. Иногда в рассмотг рение вюдят нормиро- ванную спектральную плотность Рж(о)), являющуюся изображением Фурье нормированной корреляционной функции (9.48): Р. И = J Р. (т) е-/» = (o))/D,. (9.66) Нормированная спектральная плотность имеет размерность времени. § 9.5. Связь между корреляционными функциями и спектральными плотностями случайного процесса на входе и выходе линейной системы Рассмотрим линейную систему автоматического управления (рис. 9.11), имеющую передаточную функцию Wgis) и импульсную переходную функцию (функцию веса) k(t). Предположим, что на вход этой системы подан стационарный случайный процесс G{t) с равным нулю средним значением, имеющий корреляционную функцию Rg{x) и спектральную плотность Sg{(i}). Если рассматриваемая линейная система устойчива и сама стационарна, то установившийся выходной сигнал X(t) также будет стационарным случайным процессом, среднее значение которого будет равно нулю, однако его статистические характеристики будут отличаться от статистических характеристик входного сигнала. X(t) Допустим, что случайный > Wgx(g),A(tj процесс X(t) имеет корреляцион- p(T)» %("} ную функцию Rx(x) и спект- : ральную плотность 5я:(со). Уста- -] Рис 9 11 новим связь между корреляционными функциями и спектральными плотностями случайных процессов на входе и выходе системы. Связь между реализациями x(t) случайного процесса X{t) на выходе системы и соответствующими реализациями q{f) Случайного процесса G(i) на вхрде системы на основании формуль! свертки выражается через импульсную пе- реходную функцию k{t) следующим образом: x{t)= J k(t~K)g(,k)dX= j" g{t~K)k{k)dK, (9.67) - oo -oo где X - независимая переменная интегрирования. Для момента времени t + х получаем x{t-\-x)= f g(/ + x-ri)fe(7i)dr), (9.68) - oo где т) - новое обозначение независимой переменной интегрирования. Корреляционная функция Rx(x) стационарного случайного процесса X{t) на основании (9.31) равна ?.W = lim--- \ x(t)xit + x)dt. (9.69) Подставляя в (9.69) значение x(t) и x{t + х) и изменяя последовательность интегрирования, получим г оо Rx (т) = lim -L Г g- (t -К) kmdK{ g{t + xTi) k (ri) drdi = ~T -oo = j k{k)dk J k(ri) gt-k)g{t + x~ri) -oo L -T dr\. Так как lim - J g(t - K) g (t + x - r\) dt = Rg (x + r-*«. 2Г -r + K - r\), окончательно получаем ОО oo • /?«(т)= J k(k)dk j fe(ri)/?g(T + X-Ti)dri. (9.70) - oo -oo Выражение (9.70) является основным интегральным соотношением, позволяющим по известной корреляционной функции Rg(x) случайного процесса на входе системы и известной импульсной переходной функции k(t) системы найти корреляционную функцию Rx(x) случайного процесса на выходе системы. Определим теперь связь между спектральными плотностями входного и выходного случайных процессов. Б срответстеии [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [ 56 ] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0014 |