
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [ 5 ] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 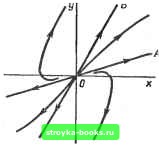 Рис. 7.16 Рис. 7.17 . Линейная апериодическая система с вязким трением. Пусть h> О, > Шо, тогда корни характеристического уравнения системы (7.13) действительны и отрицательны. В фазовой плоскости существуют прямолинейные фазовые траектории, проходящие через начало координат. В самом деле, пусть существует траектория у =kx. Найдем k. Так как для этой траектории dyldx = у/х = к, то dy/dx = k = - 2h - - ыЬх/у = - 2h - iol/k или k"" + 2hk + ш8 = 0. Таким образом, уравнение для k совпадает с характеристическим уравнением и, поскольку корни последнего вещественны, существуют прямолинейные фазовые траектории, лежащие между граничными траекториями А и В, с угловыми коэффициентами, равными значениям корней. Вид траекторий показан на рис. 7.16. Вне найденных траекторий остальные траектории имеют вид параболического типа кривых, приближающихся к началу координат и входящих в него под углами arctg {min (sj, s)}. Прямая с наименьшим по модулю угловым коэффициентом -это касательная к траекториям. Как видно из рисунка, в таких системах число перерегулирований - не более одного. Точка равновесия - начало координат - в данном случае является особой точкой типа узла. Все фазовые траектории (за исключением двух изолированных траекторий, лежащих на более круто расположенной прямой) имеют в узле общую касательную. При h<CO фазовые траектории имеют вид, показанный на рис. 7.17. Эта картина соответствует неустойчивым решениям § 7.3. Автоколебания. Метод точечных преобразований Начнем с примера. В системах с положительными обратными связями при определенных условиях могут возникать силы, приводящие к пополнению рассеиваемой на трении энергии. Б таких системах могут возникать незатухающие колебания. На рис. 7.18 изображена схема лампового генератора. Учитывая связь анодного тока с токами «l и ic, проходящими соответственно через индуктивность и конденсатор колебательного контура RLC, составим для этого контура уравнение: Ld* iUdt + Rdiddt + iUC = - iJC. характеристику лампы идеальной (рис. 7.19), Считаем т. е. О, «„<0. Сеточное напряжение уg равно напряжению вторичной обмотки трансформатора = - Mdijdt, поэтому, обозначая iL = X, RIL = 2h, \/(dC) = cog, получим x + 2hx + aioX = cog/, x>0; 0, xO. (7.16) Фазовые траектории в верхней и нижней полуплоскостях в соответствии с (7.14) представляют собой спирали, скручивающиеся к точке л; = / на оси х в верхней и к началу координат в нижней полуплоскости. 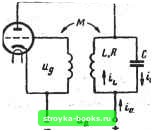 Рис. 7.18 Рис. 7.19 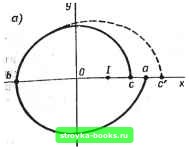
Рис. 7.20 Рассмотрим движение, начинающееся в точке Хо = а на оси X (рис. 7.20. а). Решение уравнения для фазовой траектории, выходящей из этой точки и проходящей в нижней полуплоскости, дается в (7.15). Для продолжения этой траектории в верхней полуплоскости начальными значениями будут конечные значения ху ъ момент времени = л/о. При t = t, у = О имеем х= -Хое-**= -Хре-*"/". Уравнение движения по верхней траектории X = / -f- Ле-л <-•) sin О) (t -tl) + Be- <->) cosw (/ - <,). Произвольные постоянные при поставленных начальных условиях А = (Ы(л){Ь + /), В = - (Ь Л- /), поэтому X = /-(Л/ю) (Ы-/) е-* «-•> sin (D (/-«i)- -(fc + /)e-"-)cosw(<- где b = XqC- точка пересечения траектории с осью х влево от начала координат. По истечении времени t - 2ti = = 2л/а) траектория снова пересечег ось абсцисс справа (точка с)- , Значение с равно = с= X (2л/ю) = / + (fe f /) е-""/". Обозначив е-"/™ = у, получим уравнения, связывающие а, Ь к с: Ь = уа. [0] [1] [2] [3] [4] [ 5 ] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0024 |