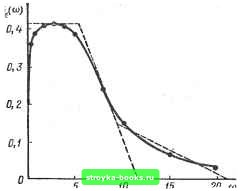Рис. 9.15

Пример 9.2. Решить предыдущую задачу графоаналитическим методом.

1. Находим выражение для спектральной плотности ошибки:

5,(w) =

jcoO+jcuT)

T{jo,r + (i(o) + K

2Dg Tg Ты* + {2DgTg + K NTg) a + KN ~ [Та* + 0-2КТ)а + КЦ(1+(йТ) "

Подставляя числовые значения параметров, получаем

(со) = (40й)4 + 400tu2 + 0,25)/ [(0, 01 со« + 25) (400со2 + 1)].

Задавая различные значения со в пределах от О до 20, вычисляем (со) и записываем результаты:

со...... О 0,1 1 2 3 5 8 10 15 20

S(o)) . . . 0,01 0,32 0.4 0,425 0,425 0,4 0,25 0,16 0,06 0,03

2. Строим график (а) (рис. 9.15), разбивая который на типовые фигуры (прямоугольники, треугольники, трапеции) находим величину площади П, ограниченной кривой (сй) и осью абсцисс:

Я= Scu)dcu = 4,7. о

3. Определяем среднее значение квадрата ошибки, равное в данном случае дисперсии ошибки:

S- (ш) d(o S

= 1,49,

и среднеквадратическое отклонение ошибки:

о =Ke- = !,22В.

Следует отметить, что рассмотренная выше задача быстрее и проще решается аналитическим методом, который к тому же позволяет установить аналитическую связь между величиной средней квадратической ошибки и параметрами системы. Приближенный графоаналитический метод интегрирования спектральной плотности целесообразно применять лишь при значениях п > 4, когда аналитический метод оказывается слишком громоздким.

Пример 9.3, Решить предыдущую задачу при условии, что на входе замкнутой системы действует регулярный полезный сигнал g(/)==a-f Vi, где о = 10 В; V = \ В/с. Случайная помеха F (t) типа «белый шум» имеет спектральную плотность Sf (<о) = N.

1. Так как полезный сигнал g (t) - регулярная функция времени, то среднее значение квадрата ошибки в соответствии с (9.94)

Р=/п(.о+с=«г(о+в7.

где {/) ~ W gf, (s) 8 С) - динамическая составляющая ошибки, обусловленная регулярным полезным сигналом g {/); = - среднее значение квадрата случайной составляющей ошибки, обусловленное случайной помехой F (t). Величина Ef была определена в примере 9.1, она равна sf = К N/2.

2. Определяй установившееся значение регулярной составляющей ошибки /Ttg (/) методом коэффициентов ошибок:

me()=cog(0 + c, -+--.f ... . . .-

Для нахождения коэффициентов ошибок Сд, с,, с, ... разложим Передаточную функцию Vlg (s) = 1/[1 + W (s)], связывающую полезный сигнал и помеху, в ряд по возрастающим степеням s, что удобно, например, сделать, разделив числитель выражения для WJs) на его знаменатель:

s + Ts 1 КГ-1

-c„-!-c,s+--s2+....;

следовательно, == 0; tl = cj2\ = (КТ - \)/К.

В нашем случае dg (t)ldt = V, а все последующие производные от полезного сигнала равны нулю. Поэтому окончательно получаем

m(t)=Q-e(t)+Ci-+ -0=Cidg(t)ldt=V/K.

3 Находим результирующее значение среднего квадрата ошибки:

Подставляя числовые значения коэффициентов, получаем

Г» = (1/5)" + (5 0,01)/2 = 0.065. Средняя квадратическая ошибка

ес.к -!К?-0.255 В.

§ 9.7. Синтез линейных систем с минимальной средней квадратической ошибкой

Рассмотрим систему автоматического управ.ления с передаточной функцией IFa (s), служащую для усиления и преобразования управляющего полезного сигнала С(/) при наличии случайной помехи F(t). Это преобразование в общем случае производится в соответствии с некоторым заданным оператором (алгоритмом преобразования) H(s) (рис. 9.16).

В общем случае система должна возможно более точно воспроизводить на своем выходе не само управляющее воздействие G{t), а некоторую функцию от управляющего воздействия

Z(/) = H{s)G(t). (9.107)

В системах, находящихся под воздействием случайного (или регулярного) полезного сигнала и случайной помехи, возникает задача отделения полезного сигнала от помехи и подавления (фильтрации) последней. Эту задачу называют

задачей фильтрации или сглаживания.

Введение преобра-зующего оператора H{s) обобщает задачу не

SjH - I p/i) только на обычные еле

дящие системы, у кото рых Z(0 = С(0 1т. е H{s) = П. но и на дру гне классы систем, вы полняющие различные преобразования управ-Рис. 9.16 ляющего сигнала.

Git)