
 |
|
Главная Нелинейные системы управления [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [ 63 ] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] в зависимости от вида оператора H{s) задача фильтрации сочетается с задачей воспроизведения [если H{s) = const], упреждения (предсказания), или экстраполяции [если H{s) = = е*], интегрирования [если H{s) = 1/s], дифференцирования [если H{s) = si и др. В общем случае преобразующий оператор (s) может быть произвольным. Идеальное преобразование полезного сигнала в соответствии с (9.107) невозможно из-за динамических ошибок системы, а также из-за наличия возмущающих воздействий (помех). Поэтому выходной сигнал (регулируемая величина) X{t) будет отличаться от воспроизводимого сигнала Z(t). Разность Е(0 = Z{t)-~X(t) (9.108) называют случайной ошибкой системы. Синтез систем при случайных воздействиях заключается в определении динамических характеристик системы, наилучшим образом обеспечивающих выполнение некоторого статистического критерия оптимальности. Существуют различные статистические критерии оптимальности. Однако наиболее часто за статистический критерий оптимальности принимают критерий минимума средней квадратической ошибки [см. (9.95) / lim-L \ e(t)dt. (9.109) где б() - любая реализация случайной ошибки. В этом случае задача синтеза состоит в том, чтобы найти такую физически реализуемую оптимальную передаточную функцию замкнутой системы Wz.om (s). при которой было бы минимальным среднее значение квадрата ошибки: e = {Z{t)-X{t)}=mm. (9.110) Согласно критерию средней квадратической ошибки оценка точности системы производится в зависимости от среднего, а не мгновенного значения ошибки, что ие всегда является достаточным, например тогда, когда требуется, чтобы ошибка не выходила за заданные пределы. Применение этого критерия может оказаться нерациональным и в тех случаях, когда требования к величине ошибки в разные моменты времени неодинаковы. Однако несмотря на то, что этот критерий, впрочем, как и всякий другой косвенный критерий, не является универсальным, он благодаря своей простоте получил широкое практическое применение. При воздействии иа систему не коррелированных между собой стационарного сигнала и помехи среднее значение квадрата ошибки состоит из двух составляющих: Если бы к системе было приложено только одно diicui-нес воздействие, либо полезный сигнал С (/), либо помеха F {{). то теоретически соотвст-стьующим выбором параметров передаточной функции (полосы пропускания) системы можно было Сы обеспечить любую точность систем. Однако при одновремепиом действии полезного сигнала и помехи томность системы не может быть любой. Это наглядно видно из рис. 9.17, где изображены (полученные ниже в примере 9.5) типичные графики зависимости составляющих ошибки е и от значении коэффициента усиления разомкнутой системы К. Для лучшего воспроизведенияуправляющего сигнала С (0. т. е. уменьшения составляющей ошибки е, система должна иметь возможно боль- 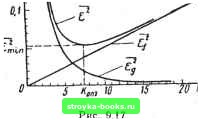 ший коэффициент усилении. Однако для того чтобы лучше подавлять помеху F (0. т- е. уменьшить составляющую ошибки е/, система, наоборот, должна иметь возможно меньший коэффициент К. Поэтому, когда па систему действуют одповреыенио полезный сигнал и помеха, существуют некоторое компромиссное (оптимальное) решение и соответствующие ему оптимальные параметры системы (в данном случае (опт). прн которых среднее значение квадрата ошибки будет мннимальиым, меиыие которого его, при заданных статистических характеристиках управляющего сигнала и помехи, никаким изменением параметров сделать нельзя. В зависимости от вида графиков спектральной плотности управляющего сигнала и помехи способы решения задачи синтеза при случайных воздействиях могут быть различны. В простейшем случае, когда спектры частот полезного сигнала 5 (<о) и помехи Sf (со) не налагаются друг иа друга (рис. 9.18, а), амплитудно-частотную характеристику замкнутой системы Л (со) выбирают достаточно широкой для обеспечения требуемой точности воспроизведения управляющего сигнала и в то же время достаточно узкой для того, чтобы система меньше реагировала на помеху. Если управляющий сиг.нал имеет спектр частот, очень быстро убывающий с возрастанием частоты, а спектр помех близок к белому шуму (рис. 9.18, б), то в этом случае форма амплитудно-частотной характеристики U(/co) разомкнутой системы должна выбираться при низких частотах, где U(/m)> 1 и сконцентрирована основная энергия управляющего сигнала, возможно более близкой к форме спектральной плотности управляющего сигнала 5(ш), а затем должна быстро убывать, по возможности следуя за убывающей характеристикой 5g(m). В общем случае, когда спектры частот полезного сигнала и помехи накладываются друг на друга и имеют произвольную форму (рис. 9.18, е), определение оптимальных параметров системы становится довольно сложным. При синтезе систем со случайными воздействиями различают два вида задач: 1. Синтез при заданной структуре системы управ.леиип, когда добиваются минимума средней квадратической ошибки, выбирая оптимальные па- а) SM A(wj раметры корректирующих звеньев системы иа основании известных статистических -характеристик полезного сигнала и помехи. 2. Синтез при произвольной структуре системы управления, когда по заданным статистическим характеристикам полезного сигнала и помехи определяют оптимальную структуру и параметры системы, при которых обеспечивается минимум средней квадратической ошибки. Синтез при заданной структуре системы. В этом случае задача синтеза формулируется следующим образом. Заданы статистические характеристики полезного сигнала и помехи, например спектральные плотности 5(м) и S,(a): структура системы н ее передаточная функция 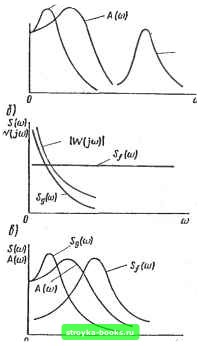 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [ 63 ] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] [164] [165] [166] 0.0013 |